上个学期到现在陆陆续续研究了一下主题模型(topic model)这个东东。何谓“主题”呢?望文生义就知道是什么意思了,就是诸如一篇文章、一段话、一个句子所表达的中心思想。不过从统计模型的角度来说, 我们是用一个特定的词频分布来刻画主题的,并认为一篇文章、一段话、一个句子是从一个概率模型中生成的。
D. M. Blei在2003年(准确地说应该是2002年)提出的LDA(Latent Dirichlet Allocation)模型(翻译成中文就是——潜在狄利克雷分配模型)让主题模型火了起来, 今年3月份我居然还发现了一个专门的LDA的R软件包(7月份有更新),可见主题模型方兴未艾呀。主题模型是一种语言模型,是对自然语言进行建模,这个在信息检索中很有用。
LDA主题模型涉及到贝叶斯理论、Dirichlet分布、多项分布、图模型、变分推断、EM算法、Gibbs抽样等知识,不是很好懂,LDA那篇30 页的文章我看了四、五遍才基本弄明白是咋回事。那篇文章其实有点老了,但是很经典,从它衍生出来的文章现在已经有n多n多了。主题模型其实也不只是LDA 了,LDA之前也有主题模型,它是之前的一个突破,它之后也有很多对它进行改进的主题模型。需要注意的是,LDA也是有名的Linear Discriminant Analysis(线性判别分析)的缩写。
LDA是一种非监督机器学习技术,可以用来识别大规模文档集(document collection)或语料库(corpus)中潜藏的主题信息。它采用了词袋(bag of words)的方法,这种方法将每一篇文档视为一个词频向量,从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序,这简化了问题的复杂性,同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布,而每一个主题又代表了很多单词所构成的一个概率分布。由于 Dirichlet分布随机向量各分量间的弱相关性(之所以还有点“相关”,是因为各分量之和必须为1),使得我们假想的潜在主题之间也几乎是不相关的,这与很多实际问题并不相符,从而造成了LDA的又一个遗留问题。
对于语料库中的每篇文档,LDA定义了如下生成过程(generative process):
对每一篇文档,从主题分布中抽取一个主题;
从上述被抽到的主题所对应的单词分布中抽取一个单词;
重复上述过程直至遍历文档中的每一个单词。
更形式化一点说,语料库中的每一篇文档与 \(T\)(通过反复试验等方法事先给定)个主题的一个多项分布相对应,将该多项分布记为 $\theta$。每个主题又与词汇表(vocabulary)中的 \(V\)个单词的一个多项分布相对应,将这个多项分布记为 \(\phi\)。上述词汇表是由语料库中所有文档中的所有互异单词组成,但实际建模的时候要剔除一些停用词(stopword),还要进行一些词干化(stemming)处理等。\(\theta\) 和\(\phi\)分别有一个带有超参数(hyperparameter)\(\alpha\)和\(\beta\)的Dirichlet先验分布。对于一篇文档\(d\)中的每一个单词,我们从该文档所对应的多项分布\(\theta\)中抽取一个主题\(z\),然后我们再从主题$z$所对应的多项分布\(\phi\)中抽取一个单词\(w\)。将这个过程重复\(N_d\)次,就产生了文档\(d\),这里的\(N_d\)是文档\(d\)的单词总数。这个生成过程可以用如下的图模型表示:
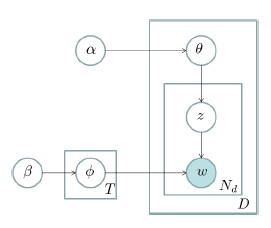
这个图模型表示法也称作“盘子表示法”(plate notation)。图中的阴影圆圈表示可观测变量(observed variable),非阴影圆圈表示潜在变量(latent variable),箭头表示两变量间的条件依赖性(conditional dependency),方框表示重复抽样,重复次数在方框的右下角。
该模型有两个参数需要推断(infer):一个是“文档-主题”分布\(\theta\),另外是\(T\)个“主题-单词”分布\(\phi\)。通过学习(learn)这两个参数,我们可以知道文档作者感兴趣的主题,以及每篇文档所涵盖的主题比例等。推断方法主要有LDA模型作者提出的变分-EM算法,还有现在常用的Gibbs抽样法。
LDA模型现在已经成为了主题建模中的一个标准。如前所述,LDA模型自从诞生之后有了蓬勃的扩展,特别是在社会网络和社会媒体研究领域最为常见。

发表/查看评论