修正的LARS算法和lasso

在小弟的上一篇文章中，简单的介绍了LARS算法是怎么回事。主要参考的是Efron等人的经典文章least angle regression。在这篇文章中，还提到了一些有趣的看法，比如如何用LARS算法来求解lasso estimate和forward stagewise estimate。这种看法将我对于模型选择的认识提升了一个层次。在这个更高的层次下看回归的变量选择过程，似乎能有一些更加创新的想法。

lasso estimate的提出是Tibshirani在1996年JRSSB上的一篇文章Regression shrinkage and selection via lasso。所谓lasso，其全称是least absolute shrinkage and selection operator。其想法可以用如下的最优化问题来表述：

在限制了$\sum_{j=1}^J|\hat{\beta_j}|\leq t$的情况下，求使得残差平和$\|y-X\hat{\beta}\|^2$达到最小的回归系数的估值。

我们熟悉如何求解限制条件为等号时，回归方程的求解。也就是用lagrange乘子法求解。但是对于这种，限制条件是不等号的情况，该如何求解，则有两种想法。第一种，也是我比较倾向于的方法，是利用计算机程序，对$t$从$0$开始，不断慢慢增加它的值，然后对每个$t$，求限制条件为等号时候的回归系数的估计，从而可以以$t$的值为横轴，作出一系列的回归系数向量的估计值，这一系列的回归系数的估计值就是lasso estimation。另外一种想法，是借助与最优化问题中的KKT条件，用某个黑箱式的算法，求解。（本人对于最优化方面的东西实在是不很熟悉，故不在此弄斧，只求抛砖引玉，能有高手给出这种想法的具体介绍。）

lasso estimate具有shrinkage和selection两种功能，shrinkage这个不用多讲，本科期间学过回归分析的同学应该都知道岭估计会有shrinkage的功效，lasso也同样。关于selection功能，Tibshirani提出，当$t$值小到一定程度的时候，lasso estimate会使得某些回归系数的估值是$0$，这确实是起到了变量选择的作用。当$t$不断增大时，选入回归模型的变量会逐渐增多，当$t$增大到某个值时，所有变量都入选了回归模型，这个时候得到的回归模型的系数是通常意义下的最小二乘估计。从这个角度上来看，lasso也可以看做是一种逐步回归的过程。

在我的上一篇文章中，提到了Efron对于逐步回归的一种看法，就是在某个标准之下（比如LARS的标准就是要保证当前残差和已入选变量之间的相关系数相等，也就是当前残差在已入选变量的构成空间中的投影，是那些变量的角平分线）选择一条solution path，在这个solution path上proceed，不断吸收新的变量进入，然后调整solution path 继续proceed。那么对于求解lasso的算法，也有一个相应的对应。Efron提出了一种修正的LARS算法，可以用修正的LARS算法来求解所有的lasso estimates。下面我介绍一下这种修正的LARS算法。

首先假设我们已经完成了几步LARS steps。这时候，我们已经有了一个回归变量集，我们记这个回归变量集为$X_{\mathscr{A}}$。这个集合就对应着一个对于$Y$的估计，我们记为$\hat{\mu}_{\mathscr{A}}$。这个估值对应着一个lasso方法对于响应的估值（这里我认为LARS估值和lasso估值应该是一样的），lasso的估值，对应着回归系数的lasso估值，回归系数向量的lasso估值我们记为$\hat{\beta}$。

为了继续进行下一步，我们先给出一个向量的表达式，然后再解释一下它

$$ w_{A}=(1_{A}'(X_{A}’X_{A})^{-1}1_{A})^{-\frac{1}{2}}(X_{A}’X_{A})^{-1}1_{A} $$

$X_{A}w_{A}$就是LARS算法的在当前回归变量集下的solution path。那么我们可以把$w_{A}$作为$\beta$的proceed的path。Efron定义了一个向量$\hat{d}$,这个向量的元素是$s_jw_j$,其中$s_j$是入选变量$x_j$与当前残差的相关系数的符号，也是$\hat{\beta_j}$的符号。对于没有入选的变量，他们对应在$\hat{d}$中的元素为0。也就是对应着 $\mu(r)=X\beta(r)$，我们有

$$ \beta_j(r)=\hat{\beta_j}+r\hat{d_j} $$

将LARS的solution path对应到lasso estimate的path上，这种对应的想法非常值得借鉴。

很显然，$\beta_j(r)$会在$r_j=-\hat{\beta_j}/\hat{d_j}$处变号。那么对于我们已经有的lasso estimate $\beta(r)$,它中的元素会在最小的的那个大于$0$的$r_j$处变号。我们记之为$\bar{r}$。如果没有$r_j$大于$0$,那么$\bar{r}$就记为无穷大。

对于LARS本身而言，在已经有了如今的回归变量集和当前残差的基础上，我们就会有条solution path，在这个solution path上proceed的最大步记为$\hat{r}$.通过比较$\hat{r}$和$\bar{r}$就会有进一步的想法。Efron的文章证明了如果$\bar{r}$小于$\hat{r}$，则对应于LARS估计的那个$\beta_j(r)$不会成为一个lasso estimation。（这个是因为当前残差和对应变量的相关系数的符号一定是和该变量的系数符号一致才行）。在这种情况下，我们就不能继续在LARS的solution path上继续前进了，为了利用LARS算法求得lasso estimate，Efron提出把$\bar{r}$所对应的那个$r_j$所对应的$x_j$从回归变量中去掉。去掉之后再计算当前残差和当前这些变量集之间的相关系数，从而确定一条新的solution path，继续进行LARS step。这样进行下去，可以通过LARS算法得到所有的lasso estimate。

这个对于LARS的lasso修正算法，被Efron称作“one at a time”条件，也就是每一步都要增加或删掉一个变量。下图显示了用修正了的LARS算法求lasso estimate的过程。

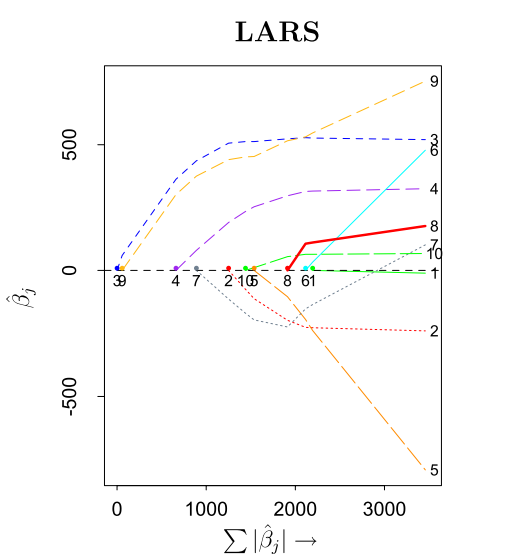
这个图是Efron等人的文章中，对于一个实际数据进行回归得到的。该数据一共有10个变量。图的横轴，是所有回归系数估值的绝对值之和，这个值从$0$增加。左侧的纵轴，是回归系数的估值，右侧纵轴是这些回归系数对应的变量的下标。这个图中，我们可以看到每一个回归系数的path。可以看到第七个变量对应的回归系数在横轴快到3000的时候变为了0，说明到这一步时，该变量被删除掉，之后又被重新添加到了回归变量集中。

下面通过一个简单的模拟，对lars和lasso以及forward stagewise做一个简单的实现。其实在R中已经有了一个名为lars的包，可以实现上述三种回归。

首先，我要模拟的方程为

$$ y=x^3_1+x^2_1+x_1+\frac{1}{3}x^3_2-x^2_2+\frac{2}{3}x_2+e $$

其中$x_1$和$x_2$是服从二维联合正态分布，均值为零向量，$cov(x_1,x_2)=0.5$，$var(x_1)=var(x_2)=1$，$e$服从$N(0,9)$。我取了50次观测，然后分别通过lasso，lars，以及forward stagewise三种算法进行了回归，其变量的回归路径如下图。

简单的代码我直接贴在本文的最后。从这三个算法的图中，我们并看不出有特别的区别，只能看出一些细小的差别。至于要判断哪种算法更好，则应该因问题而异。也不是本文能够论述的问题了。

对于LARS算法的修正，还可以应用到计算forward stagewise的estimate中，在Efron的文章中也有介绍。他的这种看法，好似凌驾在整个回归变量选择过程之上，从一个更高的角度观察之，给出一种更为一般性的视角。这也就是大牛和一般人之间的差别。读Efron的文章，总有一种让人想要膜拜的冲动。对于模型选择方面的东西，值得挖掘的还很多。Tibshirani在最新的一篇综述性的文章中，给出了lasso的诞生到现今发展的一系列流程。感兴趣的读者，可以去看看这篇文章，在cos论坛上有。链接如下：

https://cos.name/cn/topic/104104

用lars算法做模拟的代码：

利用lars模拟