写了《统计学习那些事》，很多童鞋都表示喜欢，这让我越来越觉得冯导的一句话很有道理：“我的电影一向只伺候中国观众，还没想过拍给全世界人民看。这就跟献血一样，本身是好事，但如果血型不对，输进去的血也会产生排异现象。我的‘血型’就适合中国人，对不上世界观众，别到时伤了我的身子骨，还伤害了世界观众，所以我暂时不会‘献血’。”比如他的《天下无贼》，我就特别喜欢。然而天下可以无贼，却不可以没有英雄（不是张导的那个《英雄》）。今天我要写的是统计界的英雄以及英雄的故事。英雄的名字叫 EB，英雄的故事也叫 EB。

1、谁是 EB？

故事的主人公自然是 Efron Bradley(EB)。今年的 5 月 24 日，是他 74 岁生日。从他拿到 PhD 的那年算起，正好五十年。他对统计学的贡献是巨大的，必将永远载入人类史册。正如爱因斯坦所说：“方程对我而言更重要些，因为政治是为当前，而一个方程却是一种永恒的东西（Equations are more important to me, because politicsis for the present, but anequation is something for eternity）。”人生天地之间，如白驹过隙，忽然而已。然而，经典就永远是经典。若干年后，人们遥想 Efron 当年，LARS 初嫁了。雄姿英发，羽扇纶巾。谈笑间，LB¹灰飞烟灭…… 于是乎，江山如画，一时多少豪杰! 总之，LARS 的故事必然成为统计学史上的一段佳话。

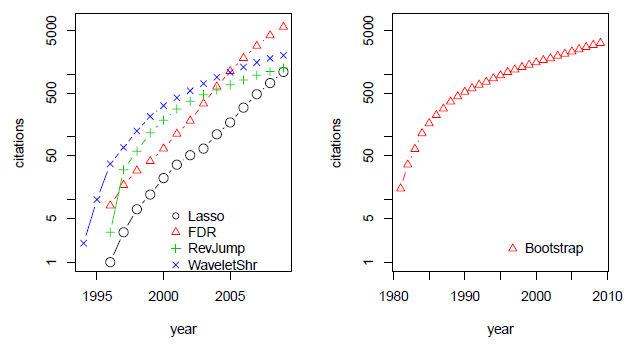
图1：此图来源于Bulhmann教授的一篇文章。右边是Efron教授的成名绝技Bootstrap。左边四个中有两个都与Efron教授有很大的关系：1.Lasso。2.FDR。

或许，对 EB 而言，至今让他回味无穷的另有其事。那就是，五十多年前，他为 Stanford 的一本幽默杂志 Chapparal 做主编。那年，他们恶搞 (parody) 了著名杂志 Playboy。估计是恶搞得太给力了，还受到当时三藩的大主教的批评。幽默的力量使 Efron 在“错误”的道路上越走越远，差点就不回 Stanford 读 PhD 了²。借用前段时间冰岛外长的语录：“Efron 从事娱乐时尚界的工作，是科学界的一大损失！”在关键时刻，Efron 在周围朋友的关心和支持下，终于回到 Stanford，开始把他的犀利与机智用在 statistics 上。告别了娱乐时尚界的 EB，从此研究成果犹如滔滔江水，连绵不绝³，citation 又如黄河泛滥，一发不可收拾，如图1所示。

2、啥是 EB？

对 Efron 教授而言，其实 LARS 只是顺手拈来，Bootstrap⁴才是他的成名绝技（他因此获得国家科学奖章，美国科学界最高荣誉）。在 20 世纪 70 年代的时候，他便把计算机引入统计学，那是具有相当的远见卓识。近年来，他更加关注的是 Large-scale Inference，所采用的核心概念便是 Empirical Bayes(EB)。这里也有很多故事，比如 Jame-Stein Estimator⁵与 Shrinkage operator 的联系⁶。

要把 EB 说清楚，得先说统计学的两派：频率派 (Frequentists) 和贝叶斯派 (Bayesians)。频率派以大规模试验下某事件出现的频率来理解概率。他们认为只要重复足够多次，事情自然就会水落石出，不需要任何人为干预，即客观性。然而，现实生活中如何判断出现某个事件的概率呢？难道动不动就要试个千八百遍？贝叶斯派说，只要有先验知识并运用贝叶斯公式 (Bayes Rule) 就行了。于是挑战者来了，“人的正确思想是从哪里来的？是从天上掉下来的吗？不是。是自己头脑里固有的吗？不是。”毛主席教导我们，“人的正确思想，只能从社会实践中来。”这就对了，Empirical Bayes（经验贝叶斯）本质上就是像贝叶斯一样分配先验分布，再利用经验数据去估计先验分布。正所谓，“enjoy the Bayesian omelet without breaking the Bayesian eggs.” Efron 教授说 EB 很好用，不管你信不信，反正我信了。

2.1 James-Stein Estimator

先来一个简约不简单的例子。现已观察到 $N$ 个 $z$ 值，即 $[z_1,z_2,\dots,z_N]$，还知道 $z_i$ 独立地来自以 $\mu_i$ 为均值，方差为 1 的正态分布，即 $z_i|\mu_i \sim \mathcal{N}(\mu_i,1)$, $i=1,2,\dots,N$. 问题是：如何从观察到的 $\mathbf{z} =[z_1,z_2,\dots,z_N]$ 估计$\boldsymbol{\mu}=[\mu_1,\mu_2,\dots,\mu_N]$？地球人都知道有一种方法去估计$\boldsymbol{\mu}=[\mu_1,\mu_2,\dots,\mu_N]$，那就是 $\hat{\boldsymbol{\mu}}=\mathbf{z}$，即 $\hat{\mu}_i = z_i,i =1, 2,\dots,N$。其实，这就是最大似然估计，记为 $\hat{\boldsymbol{\mu}}_{ML}$。现在的问题是：有没有更好的办法呢？答案是肯定的！那就是传说中的 James-Stein Estimator，

$$\begin{equation} \hat{\boldsymbol{\mu}}_{JS}=(1-\frac{N-2}{{\Vert \mathbf{z} \Vert}^2})\mathbf{z}. \end{equation}$$

只要 $N \geq 3$，$\hat{\boldsymbol{\mu}}_{JS}$ 的误差总是比 $\hat{\boldsymbol{\mu}}_{ML}$ 的误差小⁷。从公式 (1) 看，$\hat{\boldsymbol{\mu}}_{JS}$ 比 $\hat{\boldsymbol{\mu}}_{ML}$ 多了一个shrinkage:$(1-\frac{N-2}{{\Vert \mathbf{z} \Vert}^2})$，最重要的也是最有趣的是知道这个 shrinkage 怎么来的。已知$z_i|\mu_i \sim\mathcal{N}(\mu_i,1)$，即已知条件概率 $f(z_i|\mu_i)$，现在假设 $\mu_i \sim \mathcal{N}(0, \sigma^2),i = 1, \dots, N$，即假设先验概率 $g(\mu_i)$，求出后验期望 $E(\mu_i|z_i)$，并用它作为$ \mu_i$ 的估计。运用贝叶斯公式，再加上这里$f(z_i|\mu_i)$和$g(\mu_i)$都是高斯分布，我们可以解析地得到⁸:

• $z_i$的边际分布：

$$\begin{equation} z_i \sim \mathcal {N}(0, 1+\sigma^2) \end{equation}$$

• $\mu_i$的后验分布：

$$\begin{equation} \mu_i|z_i \sim \mathcal{N}\left( (1-\frac{1}{1+\sigma^2})z_i, \frac{\sigma^2}{1+\sigma^2}\right). \end{equation}$$

于是可得

$$\begin{equation} \mathbb{E}(\mu_i|z_i)=(1-\frac{1}{\sigma^2+1})z_i. \end{equation}$$

注意，这里 $\sigma^2$ 是不知道的，需要估计$\sigma^2$。经验贝叶斯就在这里起作用了，即用观察到的数据去估计 $\sigma^2$。下面需要用到统计学里面的两个常识⁹：第一，如果随机变量 $z_i,i=1,2,\dots,N$ 都独立地来自标准正态分布，那么他们的平方和服从自由度为 $N$ 的 $\chi^2$ 分布，即 $Q=\sum^N_{i=1}z^2_i\sim \chi^2_N$。第二，如果 $Q\sim \chi^2_N$ ，那么 $1/Q$服从自由度为 $N$ 的 Inverse-$\chi^2$ 分布，$\mathbb{E}(1/Q)=\frac{1}{N-2}$。现在来估计 $\sigma^2$。根据式(3)，我们知道 $\frac{z_i}{\sqrt{1+\sigma^2}}\sim \mathcal{N}(0,1)$，进一步可知 $\left(\frac{1}{\sum^N_{i=1} \frac{z^2_i}{1+\sigma^2}}\right)$ 服从 Inverse-$\chi^2$ 分布，且 $\mathbb{E}\left(\frac{1}{\sum^N_{i=1} \frac{z^2_i}{1+\sigma^2}}\right)=\frac{1}{N-2}$。 因此我们可以用 $\frac{N-2}{\sum^N_{i=1}z^2_i}$ 作为对 $\frac{1}{1+\sigma^2}$ 的估计。这样就得到神奇的 James-Stein Estimator(1)。有一点是值得注意和思考的，在估计 $\mu_i$ 的时候，James-Stein Estimator 实际上用到了所有的 $z_i$ 的信息，尽管每个 $z_i$ 都是独立的。Efron 教授把这个称为“Learning from experience of others”。

我们试着从其它角度来看这个问题。能否通过对下面这个问题的求解来估计 $\boldsymbol{\mu}$ 呢？

$$\begin{equation} \min_{\boldsymbol{\mu}} \|\mathbf{z}-\boldsymbol{\mu}\|^2 + \lambda\|\boldsymbol{\mu}\|^2 \end{equation}$$

其中 $\lambda$ 是待确定的一个参数。容易看出 $\boldsymbol{\mu}$ 有解析解：

$$\begin{equation} \boldsymbol{\mu} = \frac{1}{1+\lambda}\mathbf{z}. \end{equation}$$

式(7)是不是和式(5)惊人的相似？一个是 $\lambda$ 未知，一个是 $\sigma^2$ 未知。其实，式(6)就是频率派常用的 Ridge regression，$\lambda$ 常常通过交叉验证(Cross-validation)来确定。

还有没有其他角度呢？答案是肯定的。参见 Bishop 书 Pattern recognition and machine learning Section 3.5。做机器学习的，称这个方法为“Evidence approximation”或者“type 2 maximum likelihood”，实际上也就是经验贝叶斯。总结一下，啥叫 EB？就是像贝叶斯学派一样假设先验分布，并且利用经验数据来估计先验分布的方法，就是经验贝叶斯。贝叶斯的框架是比较容易掌握的，即假设先验分布，写出 likelihood，后验分布则正比于这二者的乘积，然后通常用 MCMC¹⁰ 来求解（当然，真正的贝叶斯高手会根据问题的特点来设计模型，加速求解）。一旦掌握这个框架，在这个框架下做事，则是不会出错的。这大概就是 Science （有规则可循，遵守这些规律就搞定）。EB 有些不同，虽然参照了贝叶斯的框架，但如何利用经验数据来估计先验分布则看个人修养了，有点像搞艺术的感觉，做得好，如同蒙拉丽莎的微笑，无价之宝；做得不好嘛，就无人问津了。下面进一步谈欣赏艺术的感受。

2.2 Tweedie’s formula

James-Stein Estimator的贝叶斯先验是这样假设的：$\mu \sim \mathcal{N}(0,\sigma^2)$（为简洁起见，从这里开始我们省略了下标 $i$）。当然也可以不这样假设，我们只需要假设存在一个分布 $g(\cdot)$，即

$$\begin{equation} \mu \sim g(\cdot),\quad z|\mu \sim \mathcal{N}(\mu,1). \end{equation}$$

可知 $z$ 的边际分布为

$$\begin{equation} f(z)=\int^{\infty}_{-\infty} \varphi(z-\mu) g(\mu) d\mu \end{equation}$$

其中，$\varphi(x)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right)$ 是标准正态分布的概率密度。$\mu$ 的后验分布为

$$\begin{equation} g(\mu|z)=\varphi(z-\mu)g(\mu)/f(z). \end{equation}$$

注意我们想知道只是 $\mathbb{E}(\mu|z)$。在见证奇迹之前，需要知道一点点指数家族(exponential family)的事。指数家族的概率密度¹¹可以写为

$$\begin{equation} h(x)=\exp(\eta x -\psi(\eta))h_0(x). \end{equation}$$

其中，$\eta$ 叫自然参数(natural paramter)，$\psi(\eta)$ 叫累积量生成函数(cumulant generating function，等会就明白啥意思了)。这些名字是挺难叫的，但是这些概念又确实重要，不取个名字更麻烦，既然大家都这么叫，就学着叫吧。来几个简单的例子，一下就明白(11)并不是那么抽象了。比如正态分布 $\mathcal{N}(\mu,1)$ 的概率密度函数，

$$\begin{equation} h(x)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^2}{2}\right)=\exp(\mu x-\frac{\mu^2}{2})\varphi(x). \end{equation}$$

比较一下式(12)与式(11)，就知道 $\eta=\mu$,$\psi(\eta)=\eta^2/2$。再比如泊松分布的概率密度函数，

$$\begin{equation} h(x) = \frac{\exp(-\mu)\mu^x}{x!}=\frac{\exp\left(\log(\mu)x-\mu\right)}{x!} \end{equation}$$

于是可知 $\eta=\log\mu,\psi(\eta)=\exp(\eta)$。好，现在回答为啥 $\psi(\eta)$ 叫矩发生函数。因为式(11)中的 $h(x)$ 是一个合法的概率密度函数，$h(x)$ 必须满足

$$\begin{equation} \exp(-\psi(\eta))\int \exp(\eta x )h_0(x) dx=1. \end{equation}$$

在式(14)两边同时对 $\eta/$ 求导，

$$\begin{equation*} -\frac{d\psi(\eta)}{\eta} \exp(-\psi(\eta))\int \exp(\eta x) h_0(x)dx + \exp(-\psi(\eta))\int \exp(\eta x) h_0(x) x dx=0.\nonumber \end{equation*}$$

根据式(14)得

$$\begin{equation} -\frac{d\psi(\eta)}{\eta} + \exp(-\psi(\eta))\int \exp(\eta x) h_0(x) x dx=0. \end{equation}$$

由式(14)还可知 $\exp(-\psi(\eta))\int \exp(\eta x) h_0(x) x dx = \int x h(x)dx =\mathbb{E}(x)$.于是式(15)可以写为

$$\begin{equation} \frac{d\psi(\eta)}{d\eta} = \mathbb{E}(x). \end{equation}$$

即对 $\psi(\eta)$ 求一阶导数，可以得到一阶矩，即期望，再继续求导下去，得到二阶矩，即方差

$$\begin{equation} \frac{d^2\psi(\eta)}{d\eta^2} = \mathbb{V}(x). \end{equation}$$

以此类推。这就是 $\psi(\eta)$ 名字的由来。

好了，见证奇迹的时候到了！式(10)可以写为

$$\begin{equation} \begin{aligned} g(\mu|z)&=\varphi(z-\mu)g(\mu)/f(z) \\ &=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(z-\mu)^2}{2}\right)g(\mu)/f(z)\\ &= \left[\exp\left(z\mu\right)\right] \left[\frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right)/f(z) \right] \left[\exp\left(-\frac{\mu^2}{2}\right)g(\mu)\right]\\ &= \left[\exp\left(z\mu -\log \frac{f(z)}{\frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right)} \right)\right] \left[\exp\left(-\frac{\mu^2}{2}\right)g(\mu)\right]. \end{aligned} \end{equation}$$

把 $z$ 可以看做自然参数，对 $\psi(z)=\log \frac{f(z)}{\frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right)}$ 关于$z$求导即可得

$$\begin{equation} \mathbb{E}(\mu|z) = z + \frac{d}{dz}\log f(z). \end{equation}$$

其中，$z$ 是最大似然估计，$\frac{d}{dz}\log f(z)$ 可以看做贝叶斯修正。式(19)被称为Tweedie’s formula。最神奇的是：Tweedie’s formula 并不包含先验分布 $g(\cdot)$，而只用到了$z$ 的边际分布 $f(z)$。接下来的事件就简单了，根据观察到的经验数据 $\mathbf{z}=[z_1,z_2,\dots,z_N]$ 直接去估计 $f(z)$。 当 $N$ 较大的时候，$f(z)$ 可以估计得很准。

3 浅草才能没马蹄

古诗云：乱花渐欲迷人眼，浅草才能没马蹄。花太多容易迷失方向，草太深则跑不了马。所以，一定要“浅”才行。

前面的数学推导，读起来肯定不流畅（我也写得累啊），尤其是对这些东西不太熟悉的童鞋。好吧，现在简单地总结一下。前面的讨论都是基于图 2 所示的结构。不同的只在于对先验分布 $g(\cdot)$ 的选取。James-Stein Estimator 假设 $g(\cdot)$ 是高斯分布，Tweedie’s formula 则没有。从这个意义上说，Tweedie’s formula 适用范围更广(flexible)，但需要较多的数据来估计 $g(\cdot)$。换一个角度说，当数据不够的时候，往往假设 $g(\cdot)$ 具有某种参数形式会更好一些。类似的情况可以比较最近邻域法和线性回归¹²：最近邻域法是非 常flexible 的，在低维数据分析中很好用，因为总是有足够数据支持这种 flexibility，但在高维情况下效果就很差。线性模型在高维数据分析中往往表现出惊人的性能，就在于它简单的结构。

总之，不能说一个模型越通用就越好，更不能说一个模型越简单就越不好。关键看什么情况下用以及怎么用！乔峰打出的少林长拳都是虎虎生威的！

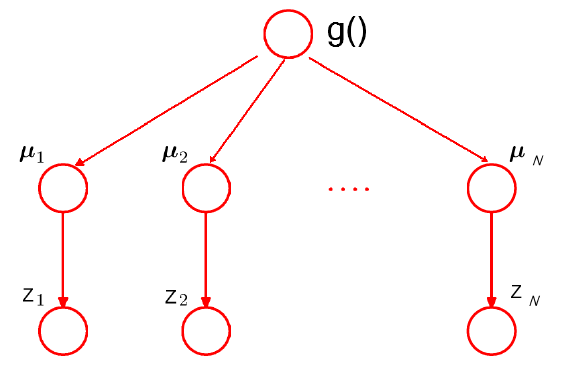
图2：James-Stein Estimator结构图。

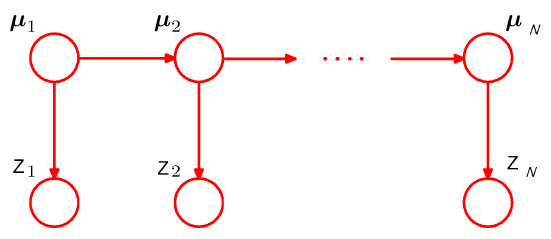
图3：HMM或者Kalman filter结构图。

现在要问的是，除了图 2 这种结构，还有没有其它结构呢？答案还是肯定的，如图 3 所示。当 $\mu$ 的状态是离散的时候，这就是著名的 HMM(Hidden Markov Model，隐马尔科夫链)；当 $\mu$ 的状态是连续的时候，这就是著名的Kalman filter （卡尔曼滤波）。值得一提的是，多层次线性模型 (Hierarchical linear models) 也源自于此，LMM(linear mixed model，昵称“林妹妹”吧)也可以有经验贝叶斯的理解，此处略去 $n$ 个字。天下武功，若说邪的，那是各有各的邪法，若说正的，则都有一种“天下武功出少林”的感觉。不管你们有没有震惊，我当时意识到“这股浩然正气”的时候，是相当震惊的。这里我还得再次表达《统计学习那些事》里面的一个观点，那就是，只有一个模型结构是不够的，还需要快速的算法去优化模型。HMM 和 Kalman filter 之所以听上去就这么如雷贯耳，还在于他们都有很好的算法。没有算法，也就没法执行，将神马都不是。掌握一个模型，除了掌握它和其它模型的联系之外，还需要掌握它的算法。如果老师只让学生学模型的大致结构，就如同赵志敬只教杨过背全真教的内功心法一样，到比武的时候，武学天才的杨过连鹿清笃都搞不定，由此可知后果是相当严重的。学算法，最好的办法就是自己亲自去试一下，试的时候就知道能不能和内功心法映证了。我记得小学时候的一篇课文《小马过河》，亲自实验的结果很可能是：“河水既没有老牛说的那么浅，也没有小松鼠说的那么深”。

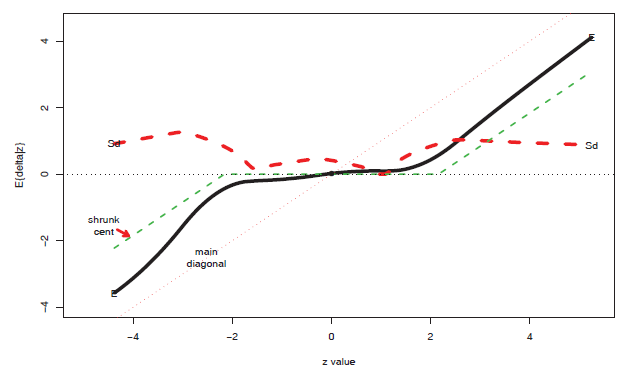
图4：经验贝叶斯（黑色实线）与shrunken centroids(绿色虚线)。红色虚线是经验贝叶斯估计的标准差。

4 神龙摆尾

2000年到2008年，Efron 教授主要致力于研究 Large-scale Inference，他有关 False Discovery Rate(FDR) 的经验贝叶斯解释，给人拨云见日的感觉。2008 年的时候，Efron 教授突然神龙摆尾，用经验贝叶斯做预测¹³。他用到了 $\mu\sim g(\cdot),z|\mu \sim \mathcal{N}(\mu,1)$，根据 Tweedie’s formula(19) 得到 $\mathbb{E}(\mu|z)$。 他观察到一个很有意思的情况：他的结果与 Tibshirani 的shrunken centroids (SC) 给出的结果很相似，如图 4 所示。我们可以看到两点吧：第一，在大规模推理 (Large-scale-inference) 时，有很多 $\mu=0$。第二，就算$\mu\neq0$，$|\mu|$ 也比实际观察到的 $|z|$ 要小。比如，实际观察到的$z=4$，不能因此认为 $\mu=4$，经验贝叶斯（Tweedie’s formula）告诉我们，$\mathbb{E}{(\mu|z)}=2.74$。同样的，$z=-4$ 时，$\mathbb{E}{(\mu|z)}=-3.1$。这表明真实情况往往没有直接观察到的情况那么极端。现实生活中，我们也会发现，网络上表扬谁或者批评谁的言论，大多都会因为偏激而失真。真实的情况往往没有歌颂的这么好，当然也不会到诋毁的那么差。一个比较理性的做法是shrink （收缩）一下，从而洞察真相。统计学为这种【中庸】的思考方式提供了强有力的支持。

图5：Shrinkage operators。

EB 与 SC 紧密相连，SC 又与 Lasso 紧密相连¹⁴。SC 有更多的假设，如 feature 之间是独立的，Lasso 更加宽松，但都用了soft-shrinkage operator(对应 $L_1$ penalty)。 当然，shrinkage operator 有很多，比较出名的还有：Hard-shrinkage operator (对应$L_0$ penalty)，Ridge-shrinkage operator(对应$L_2$ penalty)，如图 5 所示。于是我们可以看到一个五彩缤纷的 penalty 世界。近年来，各式各样的 penalty 如雨后春笋般的涌现，个人认为比较成功的有 Elastic net¹⁵和 $MC+$ penalty¹⁶。好了，最后用 Efron 教授办公室的照片(图6)来总结一下吧：那些年，我们一起追的EB。

图6：Efron office at Sequoia hall of Stanford。图片由师弟在逛Stanford时拍下。能否认出照片中的人？

5 结束语

我要这天，再遮不住我眼；要这地，再埋不了我心；要这信号，都明白我意；要那噪音，都烟消云散！

PDF下载： 那些年，我们一起追的EB