“王杨卢骆当时体，轻薄为文哂未休。 尔曹身与名俱灭，不废江河万古流。”

— 唐 杜甫《戏为六绝句》（其二）

【不要问我为啥放这首在开头，千人千面千理解吧】

深度学习：概述和一孔之见

深度学习（DL），或说深度神经网络（DNN），作为传统机器学习中神经网络（NN）、感知机（perceptron）模型的扩展延伸，正掀起铺天盖地的热潮。DNN火箭般的研究速度，在短短数年内带来了能“读懂”照片内容的图像识别系统，能和人对话到毫无PS痕迹的语音助手，能击败围棋世界冠军、引发滔滔议论的AlphaGo……DNN在众多应用领域的成功无可置疑。然而，在众多（负责任的和不负责任的）媒体宣传推波助澜下，一部分人过于乐观，觉得攻克智能奇点堡垒近在眼前；另一部分则惶惶不可终日，觉得天网统治人类行将实现。作者君对此的态度如下图所示：

• 小品里，黑土老大爷对头脑发热的白云大妈说过：“什么名人，不就是个人名？”
• 对于DNN，作者君也想说：“什么怪力乱神，不就是个计算模型？”

言归正传，如果不把DNN看成上帝/天网/人工智能终点etc.，也暂不考虑当前DL和人脑思维之间若有若无的联系，那么DNN和K-Means、主成分分析（PCA）、稀疏编码（sparse  coding或Lasso）等众多耳熟能详的模型并无二致，都属于机器学习中特征学习（feature learning）范畴。假如硬说DNN有什么不同，那么大概就在一个“深”字上。从数据x中学习特征y，如果（绝大多数）传统模型写成$y = f(x)$（即学习“一个”特征变换），DNN则可以写成$y = f_N(\cdots(f_2(f_1(x))))$ （即学习“若干个级联”的特征变换）。那么究竟什么使得DNN如此效果拔群？作者君本人归纳了三点：

1. 空前庞大的参数（parameter）量（动辄成百上千万），远远超过以往任何模型的参数数量级，使得模型对于复杂映射（mapping）的表达能力极大增强；

2. 端到端（end-to-end）的训练方式，克服了以往模型分模块训练（hierarchical）、各模块没有彼此优化的劣势；

3. 前两点主要是理念上的升华，而实际中最重要的进步，是终于找到了能有效训练这样巨大模型的一套手段。尽管这些手段（如后向传播算法）不免simple & naïve，很多也缺乏严格的证明和解释；然而在大数据的东风、GPU高性能计算的魔力、及无穷无尽的tricks（如dropout、batch normalization等）加持下，这条荆棘路还是硬生生被踏出来了。

应用上的巨大成功并不能掩盖DNN本身理论缺失、“沙上筑塔”的隐忧。传统方法的优良性质和可解释性，在DNN中损失殆尽：原因既归咎于DNN本身函数的高度非线性和非凸性，也不免受困于求解算法本身的粗糙和经验化。深度学习结构过于错综复杂、性质难以分析的“黑盒子”特质，引发了学术界的众多顾虑和好奇。从2013年开始，已经有学者陆续从不同的角度，研究DNN和各类传统机器学习模型之间（如小波分析、稀疏表示、高斯过程、条件随机场 ）的内在关系，以期理解DNN的工作原理，甚至可能从传统模型的分析方法中掘得金矿，为DNN的理论框架添砖加瓦。本文以下，仅撷沧海之一珠，主要从稀疏编码（sparse  coding）角度，初步分析和解释DNN中的一些经验性成功。

从正则回归模型谈起

让我们暂时忘记DNN，从下面这个简单的带正则项（线性）回归模型看起：

$$Y=\arg\min ||X-DY||^2 +r(Y)$$

其中$X$是输入数据，$Y$是带求解的特征，$D$是表示基（basis）。$Y$除了要求相对于$D$能很好地表示（重建）$X$外，还受到一个额外正则项$r(Y)$的约束。注意这个模型看似简单，实则众多著名模型（PCA，LDA, sparse coding, etc.）都可以看成其具体例子。以上模型的求解算法可以写成一个迭代的一般表示形式 (k = 0, 1, 2,…)：

$$Y^{(k+1)}=N(L_1(X)+L_2(Y^{(k)})$$

$Y^{(k)}$是k-iteration的输出，$L_1$、$L_2$、$N$是三个变换算子。这一迭代算法可以等价表示成下图中带反馈系统的形式（目标是求解系统不动点）：

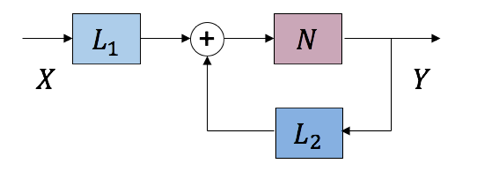
对上图反馈循环形式，我们接着做前向展开（unfolding），获得一个有无限个前向传播单元的级联结构；然后再将这个结构截断（truncate），获得一个固定长度的前向结构：

上图即是一个“展开&截断”后的前向结构示意图（到$k=2$）。首先，这一结构避免了环形结构/反馈回路的出现，所有信息流都是前向的。其次，读者可以顺着信息前进方向，逐步写出关系式（例如每个N的输入），不难发现这一结构等价于将原有迭代算法做k步近似，获得一个有限固定迭代步数下“不精确”的回归解。更有趣的是，在很多例子中，$L_1$、$L_2$是带参数的线性变换，而$N$是不带参数的非线性变换。我们注意到，这和DNN的结构形成了精妙的巧合对应：如果将$L_1$、$L_2$看做是DNN中可以训练的“层”（layer），看做DNN中的非线性操作如神经元（neuron）或池化（pooling），那么以上“展开&截断”后的前向结构（到k=2）完全可以看做一个$k+1$层、有一定特殊结构的DNN。

当然，我们也可以考虑卷积（convolution）情况下的带正则回归问题：

$$Y=\arg\min \parallel X-\sum_i F_i*Z\parallel^2 +\sum_i r(Z_i) $$

这一问题的形式、解法和结论都和前面的线性回归模型相仿。事实上，线性回归模型的结论将自然对应DNN的全连接层，而卷积回归模型的结论将对应到DNN的卷积层。

深度网络中潜藏的稀疏表示

现在，我们考虑引入1范数约束的稀疏性作为回归模型的正则项：

$$Y= \arg\min \parallel X – DY\parallel ^2 + c\parallel Y\parallel_1$$

上式是经典的稀疏表示问题。对应的迭代算法形式如下：

$$Y^{(k+1)}=N(L_1(X)+L_2(Y^{(k)})),  L_1(X)=D^TX,  L_2(Y^{(k)})=(I-D^TD)Y^{(k)}$$

则是著名的软门限算子（soft-thresholding）, 形式如下图左所示。熟悉DNN的读者可能很容易从它的形状联想到DNN中最成功的ReLU（Rectified Linear Unit）神经元，其形式如下图右所示。既然ReLU很牛，那么我们能不能把它请进我们的框架里呢？

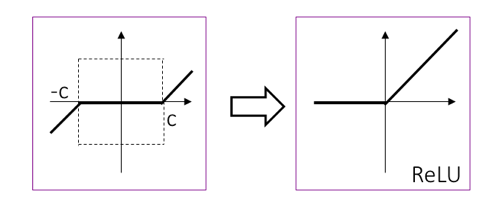
我们的策略是，加一个对$Y$的非负（non-negativity）约束到原稀疏表示问题中：

$$Y=\arg\min\parallel X-DY\parallel^2 + c\parallel Y \parallel_1,Y\ge0$$

这一约束的直接效果是把软门限算子的负半侧砍掉归0。进一步，我们可以把原本软门限算子中的门限参数c，移到线性变换当中。最后迭代形式里：

$$L_1(X) = D^TX – c, L_2(Y^{(k)}) = (I-D^TD)Y^{(k)},  N = ReLU$$

一个小问题：为什么可以“硬凑”一个非负约束到原稀疏表示问题中呢？首先“哲学”上，稀疏表达将“部分”线性组合为“整体”，如果这些“部分”还会相互抵消，总觉得不太自然  -– 当然此属怪力乱神，不听也罢。不过生物建模上，其实早将稀疏表达和神经元编码联系了起来：稀疏特征的值对应于神经元的“激发率”（firing rate,  i.e., the average number of spikes per unit time），自然而然需要非负。另外，图像处理和计算机视觉的研究者，很多都熟悉非负稀疏编码（nonnegative sparse coding, NSC）的大名；此前NSC亦是学习视觉特征的最成功方法之一。如今风水轮流转，DNN大火，经过各种神经元的经验化设计尝试、大浪淘沙，ReLU脱颖而出 。而从前的非负性和稀疏性假设经过改头换面，又于无意识间悄悄潜伏进了ReLU中；这不能不说是个有趣的发现。

再进一步，上面那个对应非负稀疏编码的“展开&截断”前向结构，如果我们想避免那些不“特别典型”的中间连接（事实上，这些“捷径”的设计正在成为DNN的新热点，参加ResNet等工作）和权重共享（被重复展开），一个选择是只保留最开始的一部分计算而删掉后面，即让迭代算法从初始值开始只跑一步近似：$Y = ReLU(D^TX – c)$：

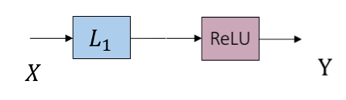
如此便获得了DNN中最典型的构成单元：全连接层 + 偏置 + 神经元ReLU。偏置 来源于原本1范数正则项的加权；在原优化问题中，调整c即调整Y的稀疏度。不难想到，如果将非负稀疏编码换成非负稀疏卷积编码，那么同样可以得到由卷积层 + 偏置 +神经元ReLU组成的单元。这一角度对一般DNN结构的分析提供了很多意味深长的提示。这里限于篇幅，不再展开。

最后，简单讲讲另外两种形式的稀疏性。其一是将稀疏编码中1范数换成0范数：

$$Y = \arg\min\parallel  X – DY\parallel^2 + c^2\parallel Y\parallel_0$$

按照以上1范数情况下的推导结果，不难解出的形式为经典的硬门限算子（hard-thresholding）。相较软门限，硬门限容易获得零值更多、更稀疏的解，常有利于分类等任务。尤其有趣的是，这一算子在2015年的国际表示学习大会（ICLR）上被DNN研究者们“经验性”地设计出来，并被冠名以thresholded linear unit；实则未免稍稍有重造轮子之憾。另一个更有意义的例子是：

$$Y = \arg\min\parallel  X – DY\parallel^2 \quad \text{s.t.} \quad \parallel Y\parallel_0 \le M$$

该问题中的约束条件可以看作池化算子（pooling）：即将输入中绝对值最大的M个值保留、其余归0。考虑到0范数约束问题是特征选择的经典形式之一，这也让我们对原本被视作单纯工程“瞎凑”的池化操作的实际作用，有了更多遐想。

总结一下，我们在这一部分都目击了些什么：

• DNN中全连接层/卷积层，和线性/卷积回归模型间的密切结构对应关系
• ReLU神经元隐含对特征“非负稀疏性”的要求
• 池化操作隐含对特征“强稀疏性”（特征选择）的要求
• 参数层偏置隐含对特征“稀疏度“的调节

总结

DNN和稀疏编码的关系深刻且本质；同样，它和其余众多传统机器学习模型间也逐渐被揭示出了千丝万缕的联系。作者组的最近工作还发掘了传统的一阶/二阶优化算法的结构，和今年大火的residual learning、fractal net等特殊网络结构和学习策略，同样有令人吃惊的精巧对应。除了作者组以外，诸如小波(wavelet)祖师Stéphane Mallat教授，压缩感知宗师Richard Baraniuk教授，约翰霍普金斯大学Rene Vidal教授，杜克大学Guillermo Sapiro教授，微软亚洲研究院Daivd Wipf博士…等多个一线研究组，近期也都对本方向投以极大关注，并陆续有优秀工作问世；方兴未艾，可以预见。 限于篇幅，无法尽述，部分参考文献列于文后以飨读者。从以往的特征工程/人工设计特征（feature engineering / crafted feature）， 走到今天的以DNN为代表的特征学习(feature learning) + 人工设计结构(crafted architecture)，到未来潜在的特征学习(feature learning) + 结构学习(architecture learning)，我们处在变革的时代，但不是“魔法”的时代；而且这变革和进步显然才到半途，亟待提升。上述工作的核心，是从传统机器学习的角度“解释”DNN中诸多经验性的结构缘何而来；在“解释“的基础上，下一步便是”分析“结构性质，和有的放矢地”创造“新的结构。作者君本人坚信，万事非偶然；这一系列经验性的对应，实实在在向我们展示了历史的螺旋上升，车轮转过同样的辐条。随着更多此类结构对应关系的发掘，将极大帮助我们理解和选择DNN的最优结构，创造新的可用结构，以及引入理论分析工具。¹

作者简介

汪张扬，男，1991年出生；2012年中国科学技术大学电子通信工程本科毕业；2016年伊利诺伊大学香槟分校电子计算机工程博士毕业；2016年加入德州A&M大学计算机科学系任助理教授。更多信息见个人主页。

拓展阅读

Sparse Coding and Deep Learning

• K. Gregor and Y. LeCun. Learning Fast Approximations of Sparse Coding, ICML 2010.
• P. Sprechmann, A. M. Bronstein, and G. Sapiro, Learning Efficient Sparse and Low Rank Models, IEEE T-PAMI, 2015.
• Z. Wang, Q. Ling, and T. Huang, Learning Deep ℓ0 Encoders, AAAI 2016.
• Z. Wang, S. Chang, J. Zhou, M. Wang and T. Huang, Learning A Task-Specific Deep Architecture for Clustering, SDM 2016.
• B. Xin, Y. Wang, W. Gao, D. Wipf, Maximal Sparsity with Deep Networks? arxiv.org
• Z. Wang, D. Liu, J. Yang, W. Han, and T. Huang, Deep Networks for Image Super-Resolution with Sparse Prior, ICCV 2015.
• Z. Wang, D. Liu, S. Chang, Q. Ling, Y. Yang and T. Huang, D3: Deep Dual-Domain Based Fast Restoration of JPEG-Compressed Images, CVPR 2016.

Beyond Sparsity: Various Interpretations of Deep Learning and Connections to classical Machine Learning Models

• J. Bruna, Joan, S. Mallat. Invariant scattering convolution networks, IEEE T-PAMI, 2013.
• A. Patel, T. Nguyen, R. G. Baraniuk. “A probabilistic theory of deep learning.” arXiv 2015.
• S. Zheng, S. Jayasumana, B. Romera-Paredes, Vi. Vineet, Z. Su, D.Du, C. Huang, and P. Torr, Conditional Random Fields as Recurrent Neural Networks, ICCV 2015.
• Z. Wang, Y. Yang, S. Chang, Q. Ling, and T. Huang, Learning A Deep ℓ∞Encoder for Hashing, IJCAI 2016.
• R. Liu, Z. Lin, W. Zhang, and Z. Su, Learning PDEs for image restoration via optimal control, ECCV 2010.
• R. Liu, G. Zhong, J. Cao, Z. Lin, S. Shan, and Z. Luo, Learning to Diffuse: A New Perspective to Design PDEs for Visual Analysis, IEEE T-PAMI,2016.
• U. Schmidt and S. Roth, Shrinkage Fields for Effective Image Restoration, CVPR 2014.
• W. Zuo, D Ren, S. Gu, L. Lin, and L. Zhang, Discriminative Learning of Iteration-wise Priors for Blind Deconvolution, CVPR 2015.
• W. Zuo, D Ren, D. Zhang, S. Gu, and L. Zhang, Learning Iteration-wise Generalized Shrinkage–Thresholding Operators for Blind Deconvolution, IEEE T-IP, 2016.
• Y. Chen, Wei Yu, T. Pock, On learning optimized reaction diffusion processes for effective image restoration, CVPR 2015.
• Y. Chen and T. Pock, Trainable Nonlinear Reaction Diffusion: A Flexible Framework for Fast and Effective Image Restoration, arxiv 2015.