统计应用

股市稳赚不亏？标普500的40年的投资回报

覃文锋

关键词：可视化; 投资; 股票

本文翻译自 GitHub 项目 zonination/investing 的描述文件 README.md。译者对原文顺序有所改动。

原文以 MIT 协议发布，已征得作者  Zoni Nation 许可进行翻译。译文版权归统计之都所有，转载请注明出处。

很多人是从 Reddit 上的 “个人理财”（/r/personalfinance）板块的贴子和评论里认识我的。 我最近也经常逛“美丽数据”（/r/dataisbeautiful）板块。 （译者注：Reddit 是一个在美国受众广泛的娱乐、社交及新闻网站。它与论坛类似，注册用户可以在网站上发布文字和链接。）

前段时间，我开始了我的第一个数据可视化项目。 我先从 Robert Shiller 的标普 500 数据项目中下载了标普 500 的一些数据，开始了疯狂的数据可视化之旅。

最近，我终于把手头上的其他几个项目处理好，安定下来，于是我又回到这些数据上，同时决定用它完成一个完整的可视化项目。

这里引用美联储主席 Alan Greenspan 对 股神 Warren Buffet 说过的一段话：

Warren，你让我太震惊了！你只要不去理会股票市场的短期甚至长期的衰退，咬紧牙关，什么也不做，不卖出任何一支股票，你就总能获得好的股票收益。 也就是，你只要把你所有的钱都投到股票里，然后回家看也不看它们一眼，之后你获得的收益比每天尝试进行股票交易的情况还要高。

“个人理财”板块上经常有人在讨论长期持仓（buy and hold）策略的资金安全问题，是选择长期持仓，还是选时操作捕捉市场（time the market）。 在这个可视化项目中，我尝试做下面三件事情：

  • 客观地回顾标普 500 相关股票的各个切面的长期投资收益（过去和现在）。
  • 验证和量化 “Invest Early and Invest Often” “早投资，勤投资” 这一格言。
  • 观察使用长期持仓策略会带来什么，以及这个策略的收益。

长期持仓收益

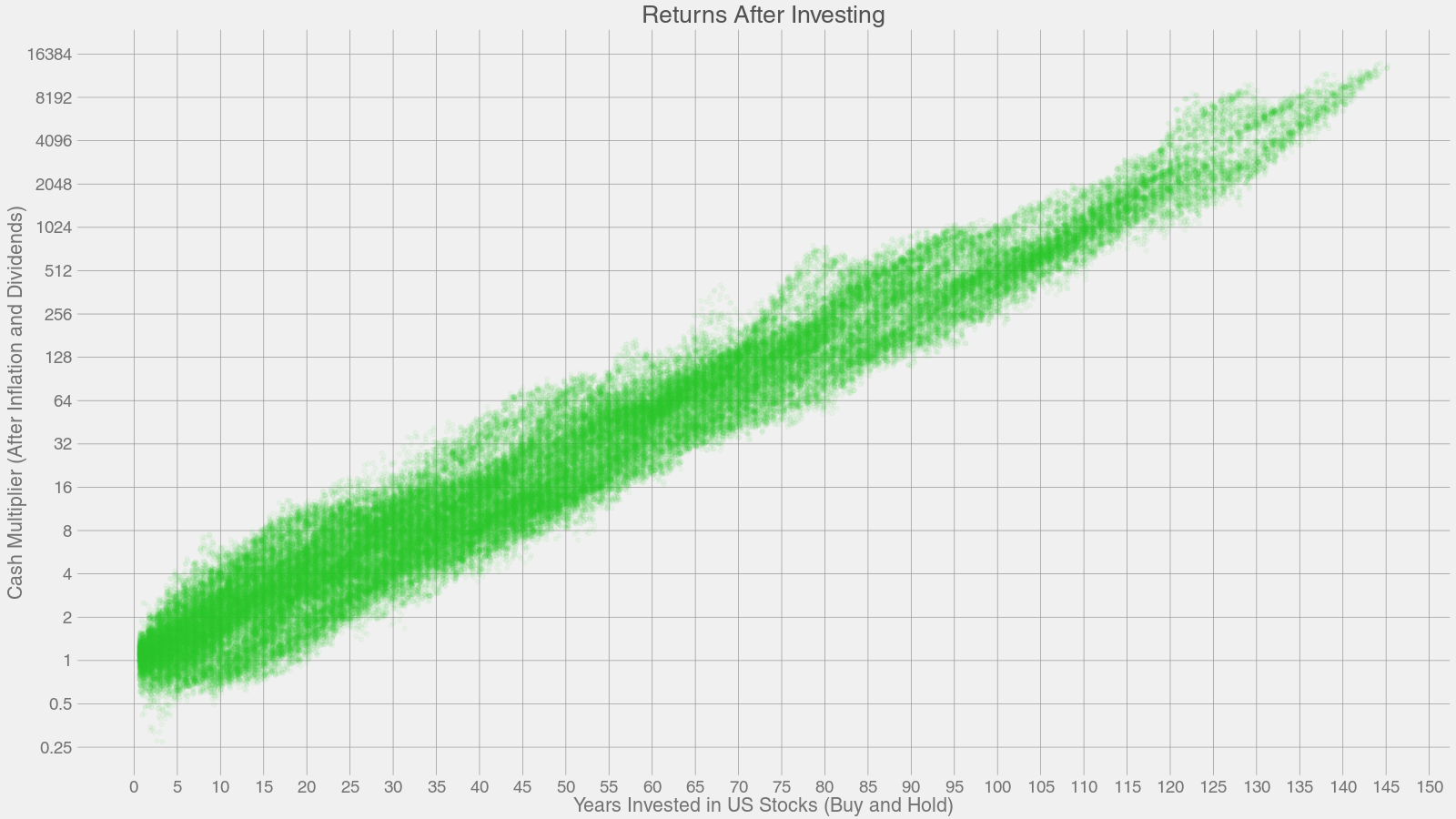
长期持仓收益

长期持仓收益与平均收益

长期持仓收益与平均收益

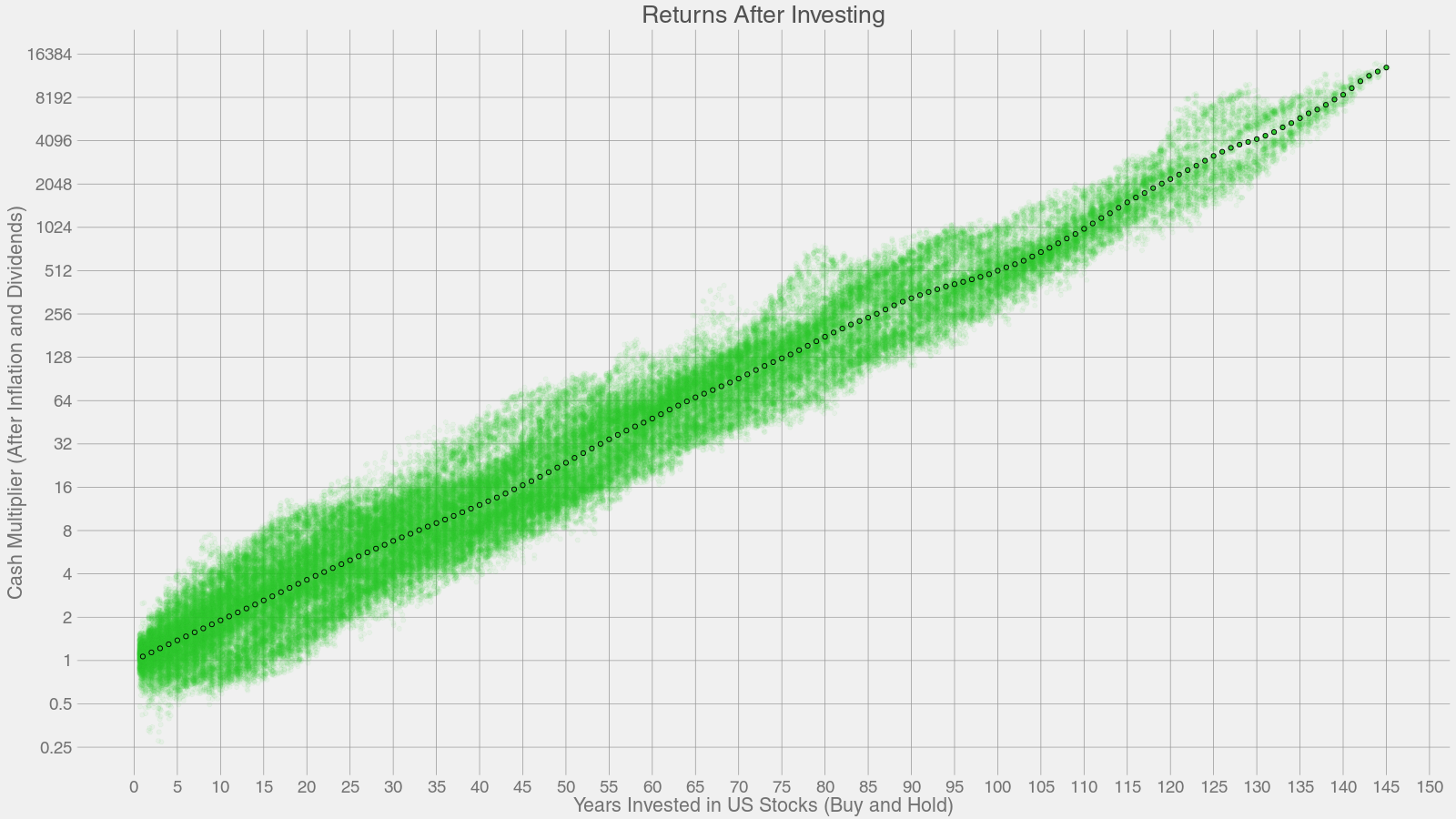
上图由标普 500 的历史收益数据生成。 在第一年，我们把标普 500 的每一支股票一年内的收益，加上股息减掉通货膨胀，把计算得到的数值作为第一年的相对收益，并以点的形状绘制到图形中。 然后，我们使用同样的方法处理第二年，第三年的数据，依次类推。具体代码见于文末，过程挺无聊的。这个程序可能会花很长一段时间来运行。

简单的说，在上图里，如果你选择投资了 X 年，你将会得到一个基于历史数据的 Y 的收益分布。

我知道了，你一定迫不及待地想问我：“等等！Zoni，这个历史长达 145 年，没有人能够活这么长时间来进行投资啊！！”

我考虑到了，因此让我们来分析一个更为实际的问题，如果你在 20 岁的时候进行投资，在 60 岁的时候退休，也就是投资 40 年的时间，结果会是怎么样的呢？ 下图就是对应的结果。

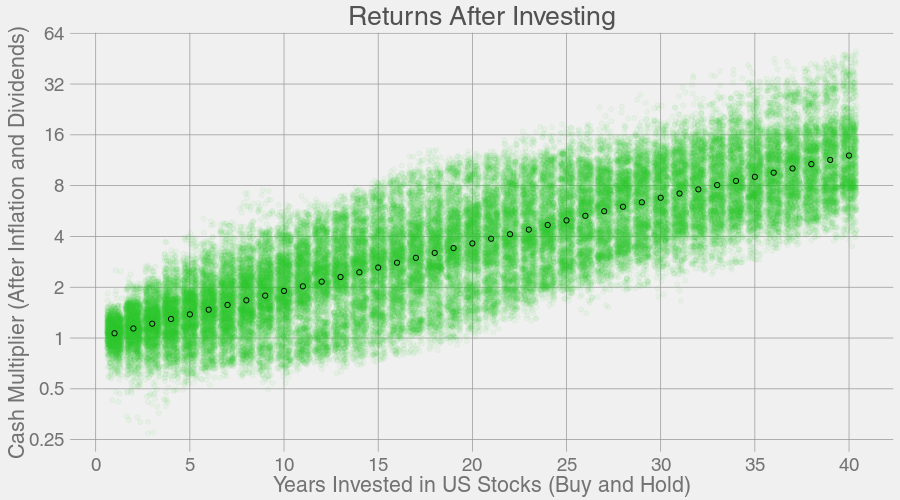
40年投资

等一下！让我们放大来看一下那些亏损的年份。

提醒一下，这些结果是收益的分布。经过1年的投资，股票可能涨了也可能跌了。经过20年投资，你几乎可以保证不会亏本。 经过 40 年的投资，你会获得很大的收益。

那每一个投资时长对应亏损的概率是多少呢？ 代码在这里，运行代码可以生成下图。

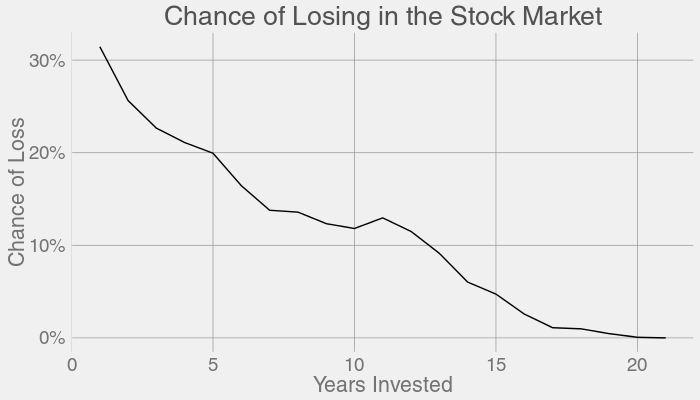
每一个投资时长对应亏损的概率

这些结果已经考虑了美国历史上历次最严重的股票崩盘，如大萧条、上世纪 70 年代的衰退、黑色星期一、互联网泡沫、2008 年金融危机等。 同时，我们注意到，股票市场都能够在这些危机的一段时间后得到完全的恢复。

下面是一个基于历史数据，使用不同时长的长期持仓策略仍然会亏损的年份。注意到，一些年份覆盖了某个特定的时期。

  • 长期持仓 10 年 (11.8%)：
    1908 1909 1910 1911 1912 1929 1930 1936 1937 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973 1998 1999 2000 2001
  • 长期持仓 15 年 (4.73%)：
    1905 1906 1907 1929 1964 1965 1966 1967 1968 1969
  • 长期持仓 20 年 (0.0664%)：
    1901
  • 长期持仓 25 年 (0%)：
    无

这些分析没有考虑到，一些年份的收益可能刚好到达平均水平，而一些年份收益可能会偏高。

让我们重新绘制之前一个图形，把Y轴的范围设置为0%到100%，可以得到下图。

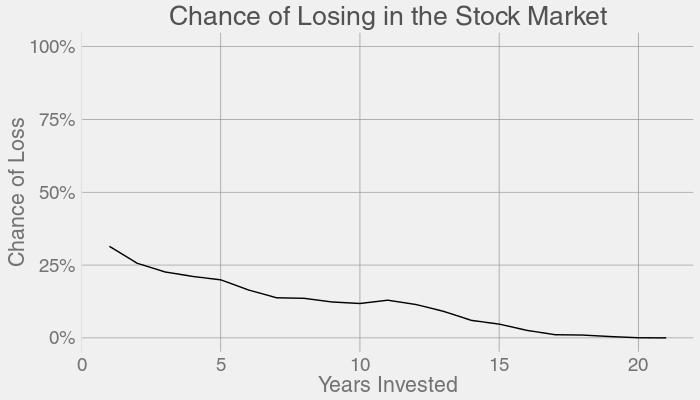
每一个投资时长对应亏损的概率0-100%

用一句话总结之前的结果，那就是：长期持仓，长期投资，而不是短期，不要选时操作捕捉市场，同时，即使你在市场高位开始投资，在长期里你仍然能够获得不错的收益。

声明

注意到，本项目模拟的股票投资组合是 100% 的美国股票。虽然很多结果显示 100% 的美国股票投资可以获得不错的收益，但是这不是一个理想的投资组合。

一个投资组合需要由一组多样化的美国股票，国际股票和债券构成。这样的多样化的投资策略能够对冲市场动荡，同时帮助投资者获得比本项目更为理想的收益。

同时，这个曲线只关注到了一次投资的一次性远期回报的问题。一个典型的投资者，通常不会选择这种方法作为长期的投资策略，而是选择平均成本投资法，分多期投入资本。（这样的策略会让曲线更为平滑。）

如果你对理财感兴趣，不妨继续阅读“深入阅读”章节的几篇文章。

常见问题

问：为什么不选择平均成本投资法（Dollar Cost Averaging ），而是选择总额投资法（Lump Sum Investing）？

答：这个问题有点难回答。我把分析的源代码都公开出来了，它们是开源的，你可以按照你想法来修改代码，进行对应的分析。同时，我还想提几点： * 在本研究中，把现金乘数（cash multiplier）作为主要的结果，就是使用无量纲的指标作为研究的结果，因此需要确定一个基期的数值。也许选择使用每年购买一份的标普 500 的股票更适合这个无量纲的问题？ * 数据中提供了通货膨胀的数据，如果你选择使用美元作为单位，你就需要考虑它。例如，怎么样对比 1992年 1 美元 和 2002 年的 1 美元的价值呢？ * 平均成本投资法需要考虑折现的问题，你需要准确地调整现有算法来反应目前使用的总额投资法的投资情况。

我的预测是，使用平均成本投资法将会使图形更加“瘦小”，让更多的数值往平均值压缩。这样会使投资更为安全一些，但是得到较慢的收益增长。

问：这个项目中的资产组合为 100% 股票？那换成债券、国际股票，或者是三者的组合会怎么样？

答：拥有这些数据是我的梦想。如果有人有类似的国际股票、债券、票据、现金、比特币或者其他类似的数值的数据，请在 Reddit 上私信我。

我希望总有一天我能分析美股、债券、国际股票混合资产的数据。

问：如果股票市场刚好在我退休的时候崩盘了，全世界都穷得响叮当，美元汇率下跌，我该怎么办？

答：好吧，下面是几个小点子：

  1. 你能够假设这个灾难真的发生了，但是你同样可以想象你的假设几乎不可能发生。真正的风险不是基于概率的，而是发生的概率乘以事件的损失程度。
  2. 不，这个灾难不是一定会发生的，快干了这碗鸡汤。
  3. 没人会建议购买 100% 的美国股票作为退休保障，而更多的是选择债券。
  4. “天快塌了”这类口吻是给会赚钱的标题党用的，跟这些人较真真是没意思。

其他可视化结果

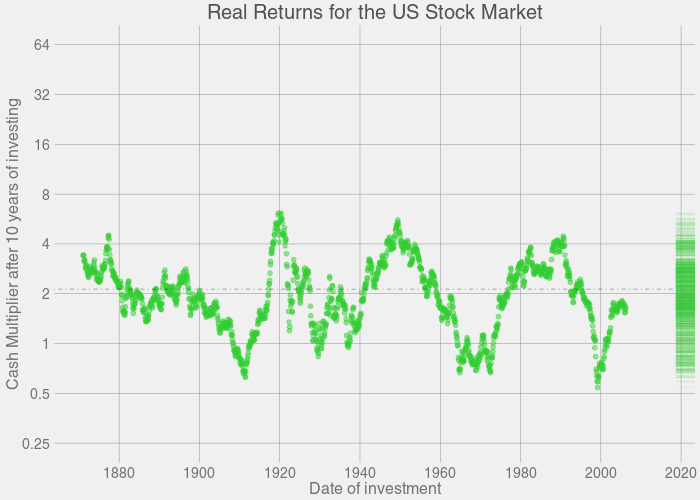
这个图形是一个动画，它展示了投资时长为某一特定年限，随着投资时长的增长，每一年的收益分布的具体变化情况。

动图

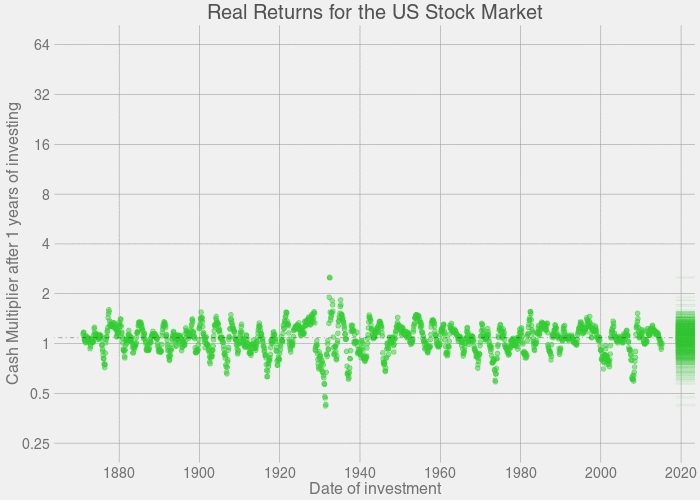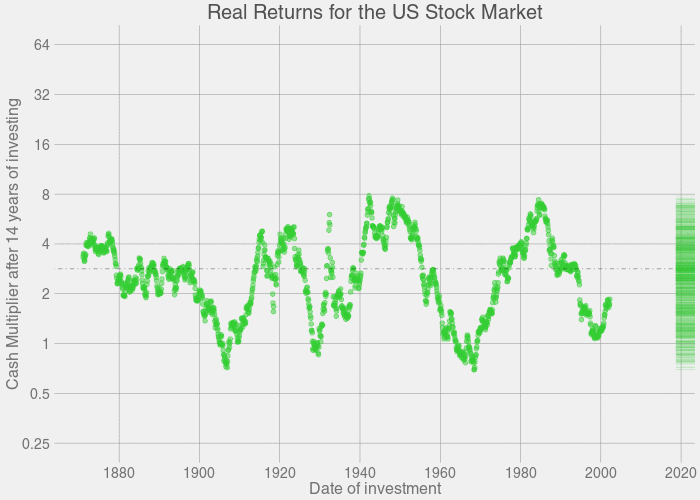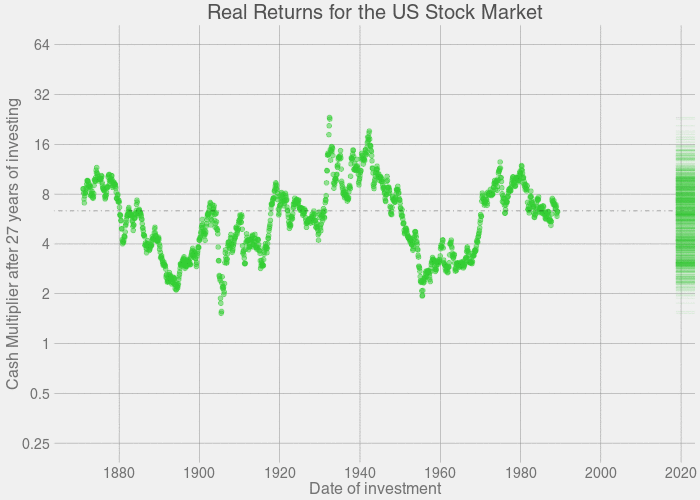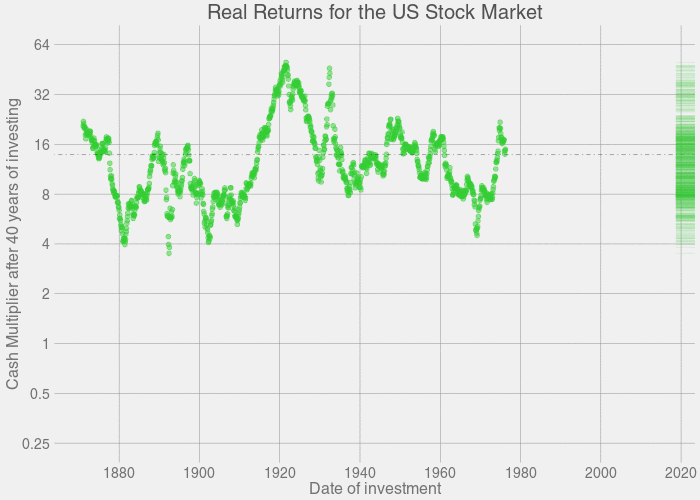
让我们逐帧地来看这个图形：

10

20

30

40

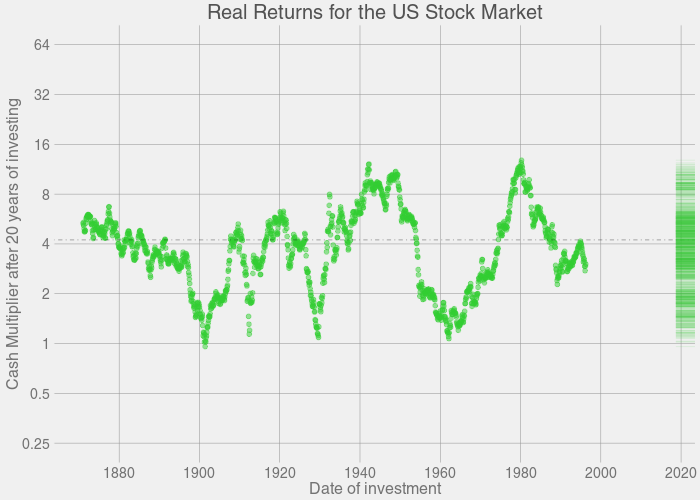
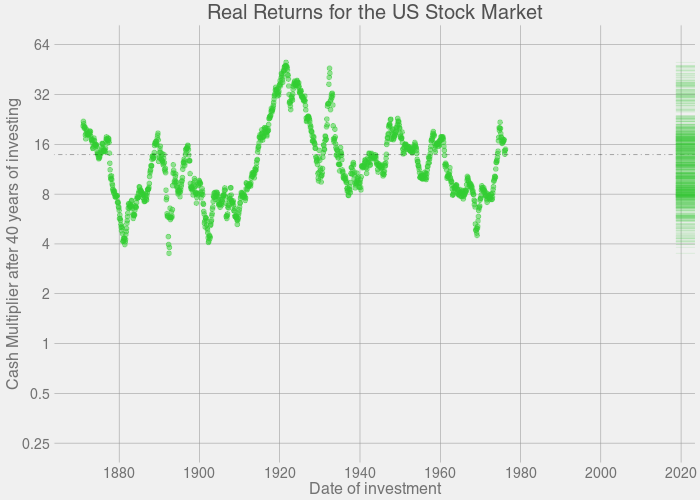
数据来源

深入阅读

源代码

# 注意：我的代码写得很垃圾，你将就着看吧

# 设置工作目录，引入对应 R 包
setwd("~/Dropbox/R/Stock Market")
library(ggplot2)
library(scales)
library(lubridate)
source("z_theme.r")

# 数据源：
# 我强烈建议使用下面的链接来获得最新的数据。
# "https://raw.githubusercontent.com/datasets/s-and-p-500/master/data/data.csv"

sp500 <- read.csv("stocks.csv", stringsAsFactors = FALSE)

# 如果你使用的数据是自行从数据源下载的，请注释掉下面这一行代码，同时取消注释下方的“主循环”代码。
stocks <- read.csv("returns.csv", stringsAsFactors = FALSE)

# 处理日期:
# 格式化日期，让 R 能够识别它们.
sp500$Date <- as.Date(sp500$Date, "%Y-%m-%d") 

# 标普 500 始于 1923 年， 其他历史数据来自于 Shiller. 如果你只想要“真实”的标普 500 历史数据，请取消下面一行代码的注释。
# sp500 <- subset(sp500, sp500$Date >= as.Date("1926-01-01", "%Y-%m-%d"))

# 计算实际收益 (所有股息都被重新投资)
sp500$real.return <- 1 # 最开始，在股票市场中投资一元
for(r in 2:nrow(sp500)){
  sp500$real.return[r] <-
    # 前一期的价格
    sp500$real.return[r-1]*
    # 乘以上一个月价格的百分比
    (((sp500$Real.Price[r] - sp500$Real.Price[r - 1])/
        (sp500$Real.Price[r - 1])) + 1) +
    # 最后加上上一个月的股息，它们被全部重新投资
    (sp500$Real.Dividend[r - 1] / sp500$Real.Price[r - 1])*
    (sp500$real.return[r - 1] / 12)
}

# 主循环 - 计算收入数据集
# 如果使用的数据是自己从数据源下载的，请取消注释下面的代码
# 警告：下面的代码会运行较长时间。
###############
# stocks <- data.frame(NA, NA, NA, NA)
# names(stocks) <- c("year", "real", "percent", "inv.year")
# for(f in 1:145){
#   sp500$future.f <- NA    #远期标普 500 价格
#   sp500$cpi.f <- NA     #远期 CPI
#   sp500$future.r <- NA  #远期实际收益
#   for(n in (f * 12 + 1):nrow(sp500)){
#     # 计算 f 年的远期价格
#     sp500$future.f[n - f * 12] <- sp500$SP500[n]                      # 远期标普 500 价格
#     sp500$cpi.f[n - f * 12] <- sp500$Consumer.Price.Index[n]          # 远期 CPI
#     sp500$future.r[n - f * 12] <- sp500$real.return[n]                # 远期实际收益
#     stocks <- rbind(stocks, c(f, sp500$future.r[n-f*12],              # 记录所有数据
#                   (sp500$future.r[n - f * 12] - sp500$real.return[n - f * 12]) /
#                     sp500$real.return[n - f * 12],
#                   year(sp500$Date[n - f * 12])
#                   ))
#   }
#   print(paste(f, " of ", 145, " completed: ", round(f/145*100,2),"%",sep=""))

# 使用现金乘数:
stocks$multip <- stocks$percent + 1
# write.table(stocks, "returns.csv") # 保存收益数据集

# 绘制图形
ggplot(subset(stocks, year <= 40&inv.year >= 1957), aes(x = year, y = multip, group = year), na.rm = T) +
# geom_boxplot(outlier.shape = NA,coef = 0,fatten = 0,fill = "steelblue", color = NA) +
  geom_jitter(color = "limegreen", alpha=.05, width = 1) +
  ggtitle("Returns After Investing") +
  stat_summary(fun.y = "mean", colour = "black", fill = "limegreen", geom = "point", shape = 21) +
  ylab("Cash Multiplier (After Inflation and Dividends)") +
  xlab("Years Invested in US Stocks (Buy and Hold)") +
  scale_y_log10(breaks = 2^c(-3:15),
                # 转化为文本，以美化图形输出结果
                labels = as.character(2^c(-3:15))) +
  scale_x_continuous(breaks = seq(0,200,5)) +
  geom_smooth() +
  z_theme()

关于作者

覃文锋

R Weekly 创始人，参与了一些的 R 包的开发，爱好是看正在用的工具的源代码。		覃文锋

敬告各位友媒，如需转载，请与统计之都小编联系（直接留言或发至邮箱：editor@cos.name），获准转载的请在显著位置注明作者和出处（转载自：统计之都），并在文章结尾处附上统计之都微信二维码。

统计之都微信二维码

发表/查看评论