本文翻译自 John Myles White 的博客 Why I’m Not a Fan of R-Squared。翻译工作已经获得作者授权同意。
本文大意
人们通常喜欢用 $R^2$ 作为评判模型拟合好坏的标准。与 MSE 和 MAD 不同,$R^2$ 不只是模型误差的函数,它的定义中还隐含了两个模型的比较:一个是当前被分析的模型,一个是所谓的常数模型,即只利用因变量均值进行预测的模型。基于此,$R^2$ 回答的是这样一个问题:“我的模型是否比一个常数模型更好?”,然而我们通常想要回答的是另一个完全不同的问题:“我的模型是否比真实的模型更差?”
通过一些人为构造的例子我们可以很容易发现,对这两个问题的回答是不可互换的。我们可以构造一个这样的例子,其中我们的模型并不比常数模型好多少,但同时它也并不比真实的模型差多少。同样,我们也可以构造出另一个例子,使得我们的模型远比常数模型要好,但也远比真实模型要差。
与所有的模型比较方法一样,$R^2$ 不单是被比较模型的函数,它也是观测数据的函数。几乎对于所有的模型,都存在一个数据集,使得常数模型与真实模型之间是无法区分开的。具体来说,当使用一个模型区分效能很低的数据集时,$R^2$ 可以任意地向零趋近——即使我们对真实模型计算 $R^2$ 也是如此。因此,我们必须始终记住,$R^2$ 并不能告诉我们模型是否是对真实模型的一个良好近似:$R^2$ 只告诉我们,我们的模型在当前的数据下是否远比一个常数模型要好。
一个例子
我们来考虑一个简单的例子,首先将备选模型与常数模型相比,然后将备选模型与真实模型对比,我们将会发现他们会产生完全相反的结论。假设我们想对函数 $f(x)$ 进行建模,它在 $x_{min}$ 和 $x_{max}$ 之间均匀分布的 $n$ 个点上又加入了噪声的观测。
我们首先假定:
$f(x)=\log(x)$$x_{min}=0.99$$x_{max}=1.01$- 在
$x_{min}$和$x_{max}$之间均匀分布的 1000 个点上,我们观测到$y_i=f(x_i)+\epsilon_i$,其中$\epsilon\sim N(0,\sigma^2)$.
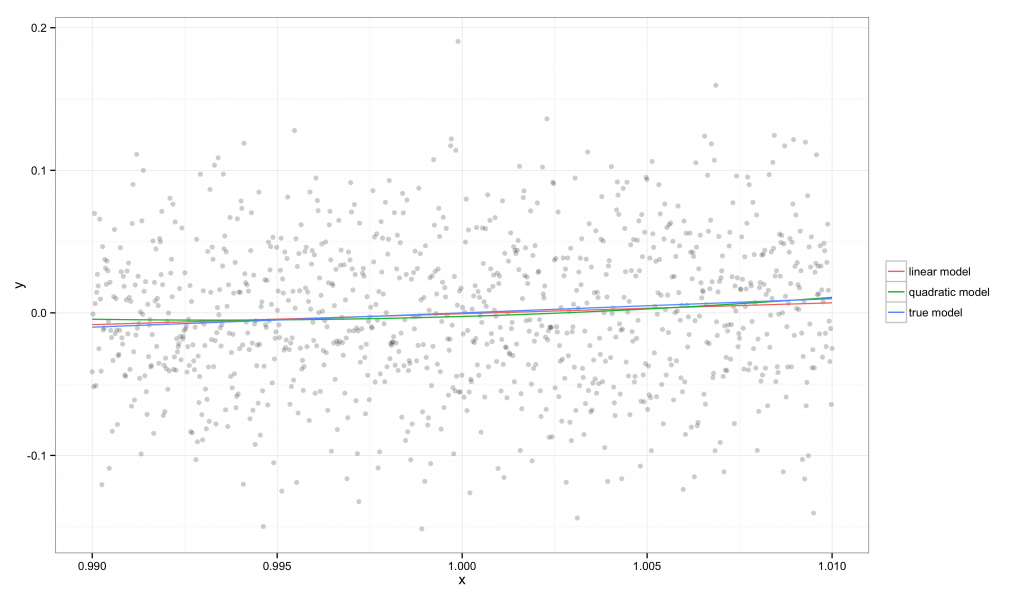
基于这组数据,我们尝试利用单变量普通线性回归来学习 $f(x)$。我们先后拟合一个线性模型和一个二次模型。下面展示了两个模型的拟合结果:
 在图中,我们可以看到
在图中,我们可以看到 $f(x)$ 可以被一条直线很好地近似,所以我们的线性和二次回归模型都可以很好地还原真实模型。这是因为 $x_{min}$ 和 $x_{max}$ 非常接近,因此真实的函数在这个区域中可以被直线很好地近似,特别是相对于我们观测的噪声水平而言。
我们可以通过两组模型比较来对这些简单回归的效果进行评判:一组是我们的模型与常数模型的对比,另一组是我们的模型与真实的对数函数模型的对比。为了简化计算,我们采用不对回归变量数目进行调整的 $R^2$ 定义,因此模型 $m$(相对于常数模型 $c$)的 $R^2$ 计算方法是
$$R^2 = \frac{\text{MSE}_c – \text{MSE}_m}{\text{MSE}_c} = 1 – \frac{\text{MSE}_m}{\text{MSE}_c}$$
与“官方”的 $R^2$ 定义一样,这个数值告诉我们,在常数模型留下的残差中,有多大的比例是为备选模型所解释的。这个比较可能会与备选模型和真实模型之间的比较得出不同的结论。为了展示这一点,接下来我们考察一个 $R^2$ 的变种,我们称之为 $E^2$,它衡量了备选模型的误差相对于真实模型 $t$ 而言有多差:
$$E^2 = \frac{\text{MSE}_m – \text{MSE}_t}{\text{MSE}_t} = \frac{\text{MSE}_m}{\text{MSE}_t} – 1$$
注意,$E^2$ 在意义上与 $R^2$ 是相反的:拟合更好的模型具有更小的 $E^2$ 取值。
在我们的例子中,可以计算出线性模型的 $R^2=0.007$,而真实模型的是 $R^2=0.006$。相对而言,线性模型的 $E^2=-0.0008$,这说明对于这组数据,备选模型与真实模型之间是很难区分开的。尽管 $R^2$ 表明我们的模型可能不是非常好,但 $E^2$ 的取值说明在当前 $x$ 的范围内,我们的备选模型已经接近完美了。
那么当 $x_{max}$ 与 $x_{min}$ 之间的间隔变大之后会发生什么呢?对于单调函数,如 $f(x)=\log(x)$,我们将发现 $E^2$ 会随着间隔的增加而增加,而 $R^2$ 的表现则非常奇特:它先会递增一会儿,然后再下降。
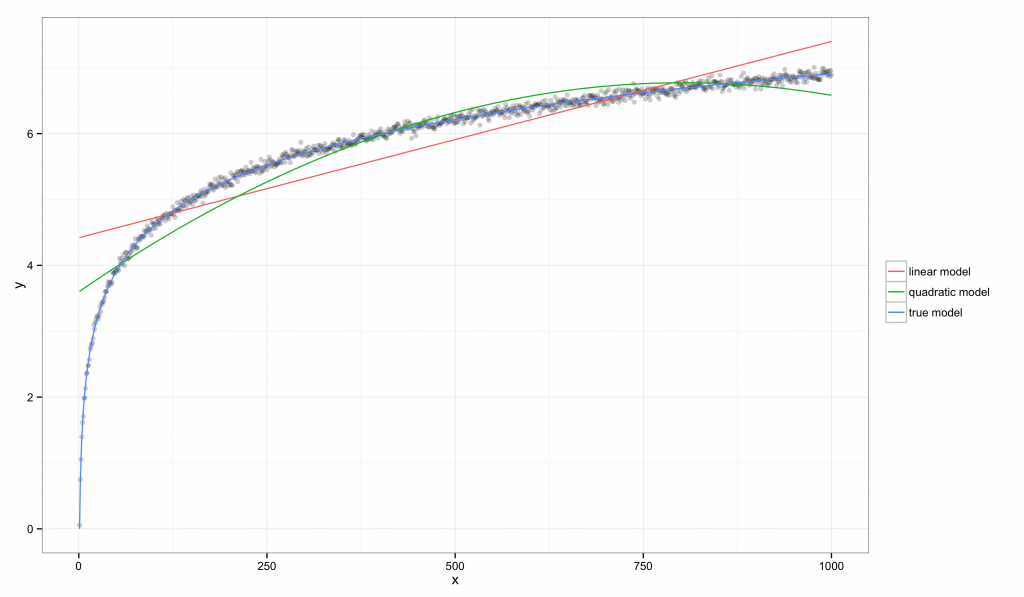
在考虑一般的情形之前,我们先看一个具体的例子,设定 $x_{min}=1$,$x_{max}=1000$:
 在这个例子中,可以通过上图看出线性模型和二次模型都有系统性的偏差,但它们的
在这个例子中,可以通过上图看出线性模型和二次模型都有系统性的偏差,但它们的 $R^2$ 值都有显著的增长:线性模型是 $R^2=0.760$,真实模型是 $R^2=0.997$。相比较而言,线性模型的 $E^2=85.582$,这说明该数据集提供了有力的证据表明线性模型比真实模型要差。
这个例子说明,尽管大多数人都会同意线性模型对真实模型的近似效果是越来越差的,但 $R^2$ 却有了显著的增长。从前一个例子到后一个的转换过程中,$R^2$ 看似得到了提升,$E^2$ 却表明由于 $x_{min}=1$ 和 $x_{max}$ 之间的间隔增加了,备选模型的拟合效果是大打折扣的。这表明 $R^2$ 并不能解释为 $E^2$ 的一个替代量($E^2$ 依赖于真实模型,通常是不可测量的)。然而我们的两个极端例子还不是故事的全部:事实上,$R^2$ 从前一个例子到后一个的转换过程中,其变化并不是单调的。
我们进行一项跟之前类似的分析,从 $(x_{min},x_{max})=(1,1.1)$ 开始到 $(x_{min},x_{max})=(1,1000)$ 结束,但考虑间隔在这其中的多个取值情形。如果我们依次计算每种情形下的 $R^2$ 和 $E^2$,那么将会得到如下的图形(对 x 轴进行了对数变换,以使曲线的非单调性更加明显)。
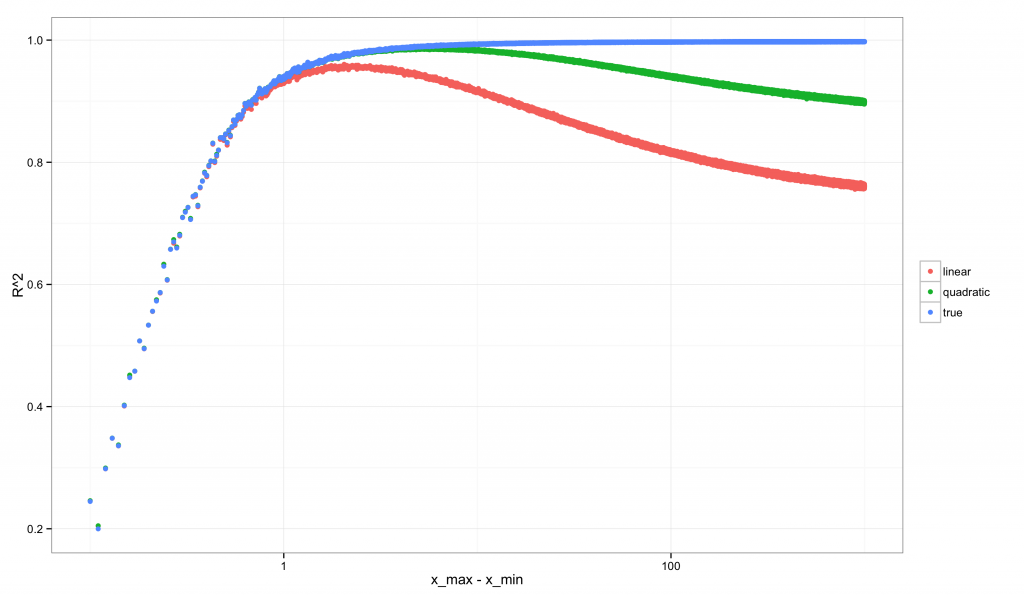
首先是 $R^2$ 的图像:
 其次是
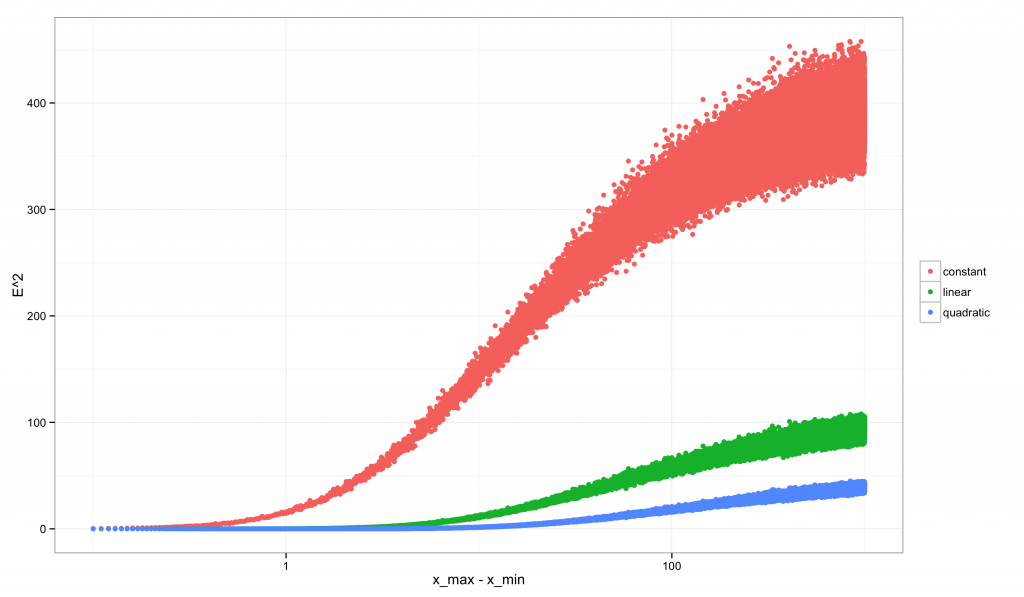
其次是 $E^2$ 的:
 注意到
注意到 $R^2$ 的图像相对于 $E^2$ 而言是多么的奇特。$E^2$ 始终是递增的:随着间隔的增加我们拥有更多可以区分模型的数据时,我们同时也拥有越来越强的证据表明线性近似不是正确的模型。相反,$R^2$ 一开始非常低(也正是 $E^2$ 很低的时候,因为我们的线性模型略差于真实模型),之后以非单调的模式发生变化:它的峰值位于当数据有足够的变异来排除常数模型,但还不足以排除线性模型的时候。在这个临界点之后,$R^2$ 就开始下降。对于二次模型,$R^2$ 的取值具有类似的非单调性。只有真实的模型展现出单调递增的 $R^2$。
结论
我写这篇文章的目的不是希望大家放弃使用 $R^2$,事实上我也一直时常需要用到它,但我认为理解以下这两点是非常重要的:(1) $R^2$ 的取值很大程度上依赖于数据集;(2) 即使你的模型在逐渐向真实模型靠近,$R^2$ 却可能会变小。在决定一个模型是否有用时,一个很高 $R^2$ 的模型也可能不理想,而反之一个具有很低 $R^2$ 的模型也有可能是非常好的。
这是一个不可回避的问题:一个错误的模型是否有用,总是和它被应用的范围,以及在这个范围内我们评价所有误差的方式有关。由于 $R^2$ 隐含了对两个模型的比较,所以一般而言它会依赖于具体的数据集。$E^2$ 同样有所依赖,但至少它不会随着回归变量 $x$ 变异的增大而呈现出非单调性的变化。
代码
文章的代码托管在 GitHub 上。
补记一
回顾这篇文章的时候,我发现当时应该更加明确地指出,像 MSE 和 MAD 这样的模型拟合评判标准也是与模型的应用范围有关的。我之所以更倾向于使用它们,是因为它们没有隐含的归一化过程,也就是说它们看上去可以是任意的数,这意味着它们对于模型的应用范围是非常敏感的——反观 $R^2$,由于它是一个归一化的数字,因此它显得不那么“任意”,这可能会让我们忘了它是非常依赖于数据的。
其次,我之前确实应该用一种不同的归一化方法来定义 $E^2$。对于模型 $m$,当拿它与常数模型 $c$ 和真实模型 $t$ 相比较时,下面这个有界的数值可能使用起来更为简便:
$$E^2 = \frac{\text{MSE}_m – \text{MSE}_t}{\text{MSE}_c – \text{MSE}_t}$$
这个数值的意义是,在较差的基准模型($\text{MSE}_c – \text{MSE}_t$)到最好的模型($\text{MSE}_t – \text{MSE}_t=0$)之间,当前模型所处的位置是哪里。注意到在之前考察的同方差回归模型中,$\text{MSE}_t=\sigma^2$,它可以从经验数据利用同方差的可识别性假定和任意固定回归变量 $x$ 上的重复观测进行估计。
此外,为了保证这个数值在 $[0,1]$ 之间,我们可能还需要加上一些额外的限制。这是因为当待比较的模型没有嵌套关系时,其取值就有可能超出范围。(在线性回归的设定中,其取值一定不会超出 $[0,1]$,因为常数模型几乎总是嵌套于更复杂的模型)。
补记二
在我睡醒看到这篇博客被转发到 Hacker News 上后,我意识到或许应该加上一些图形化的表示,以帮助那些没有理论统计背景的读者理解本文的核心思想。下面这张图表明,给定三个进行比较的模型,我们总可以在最差的模型(即常数模型)到最好的模型(即真实模型)之间找到备选模型的位置。
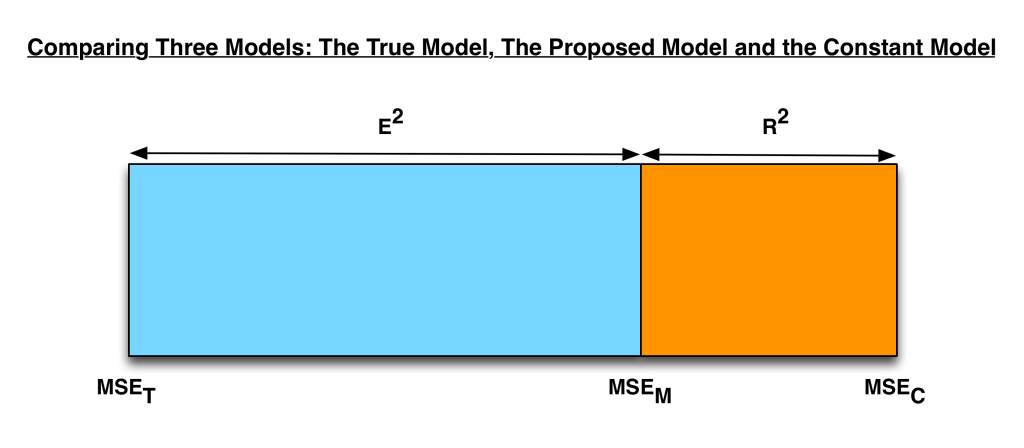 在测量备选模型所处的位置时,
在测量备选模型所处的位置时,$R^2$ 和 $E^2$ 是互补的关系。
补记三
另一种对这些想法的表达是将其中涉及到的数量进行偏差/方差分解。在这种视角下,我们可以得到
$$R^2 = 1 – \frac{\text{MSE}_m}{\text{MSE}_c} = 1 – \frac{\text{bias}_m^2 + \sigma^2}{\text{bias}_c^2 + \sigma^2}$$
而补记一中的 $E^2$ 定义则有
$$E^2 = \frac{\text{MSE}_m – \text{MSE}_t}{\text{MSE}_c – \text{MSE}_t} = \frac{(\text{bias}_m^2 + \sigma^2) – (\text{bias}_t^2 + \sigma^2)} {(\text{bias}_c^2 + \sigma^2) – (\text{bias}_t^2 + \sigma^2)} = \frac{\text{bias}_m^2 – \text{bias}_t^2}{\text{bias}_c^2 – \text{bias}_t^2} = \frac{\text{bias}_m^2 – 0}{\text{bias}_c^2 – 0} = \frac{\text{bias}_m^2}{\text{bias}_c^2}$$
在很大程度上,我认为 $R^2$ 难以理解的地方就在于其表达式中分子分母都含有 $\sigma^2$ 项。而 $E^2$ 本质上就是移除了 $\sigma^2$ 之后的结果。我认为这对于理解模型的拟合效果是更有帮助的。
作者简介:
John Myles White,Facebook 核心数据科学团队成员,加入 Facebook 之前获得普林斯顿大学心理系博士学位,并在麻省理工学院从事 Julia 编程语言的开发。

发表/查看评论