本文翻译自Aran Lunzer 和 Amelia McNamara发布的文章Exploring Histograms。翻译工作已获得作者授权同意。文中描述的交互式直方图可以前往原文链接查看。

直方图有什么难的？

直方图是对数值变量进行展示的一种可视化方法， 它使用区间汇总计数将数据集的整体分布展示出来。 但是，直方图的展示效果对绘图参数的变化很敏感。 下文我们将通过丰富的可视化效果来一步步讲解如何绘制漂亮的直方图。 如果阅读后还有不明白的地方，可以通过文末的联系方式联系我们，同时也欢迎任何意见与建议。

数据可视化

数据可视化能帮助我们更好的理解变量整体分布与变量间的关系。但由人类制作和解释的图像总是有可能存在误导性和迷惑性，典型的有感知问题和轴问题。

在这篇文章中，我们将专注于单个变量的分布。其可视化方式取决于该变量是分类变量还是数值变量。

分类变量及其分布

分类变量只会有少量特定的取值。比如“性别”就是一个常见的分类变量，只包含“男性”、“女性”和“性别不明”三种。 我们通常使用条形图来可视化一个分类变量。条形图会显示每一组类别中每一项的计数数量。下图是fivethirtyeight上统计Bob Ross绘画作品特征的条形图。一类绘画特征出现与否是离散的变量，所以Walt Hickey(图的作者)统计了包含每种元素的作品数量占总数的比例并用条形图展现出来。

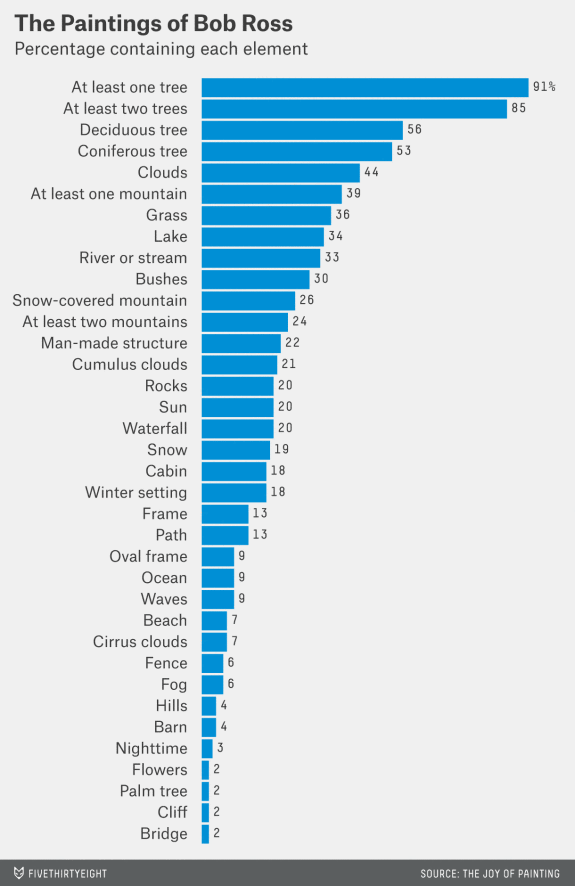
由于数据的离散性，分析师在绘制条形图时没有太多需要决定的参数，只要选择类别的排序，图形的配色和宽高比就足够了。等到对数值型变量绘制直方图时，我们会看到更多的可选参数。

数据可视化的圈子里有一伙人认为任何东西都可以用条形图展示。这可能是真的，但那样的世界是多么无趣啊！

-Amanda Cox, The Upshot.

数值变量及其分布

数值变量是以数字来度量的量。 高度是数值，通常以厘米或英寸为单位。 年龄是数值，以年或日计算。 数值变量可以是离散的或连续的。 离散变量只取整数值（1，2，3等）。 连续变量则可能取数轴上的任何值。

当一个变量是数值时，它的分布可以用各种方式表示; 可能最常用的方法是直方图。

下图是The Upshot的justin Wolfers制作的直方图，显示了1000万马拉松选手跑完全程所用时间的分布情况。

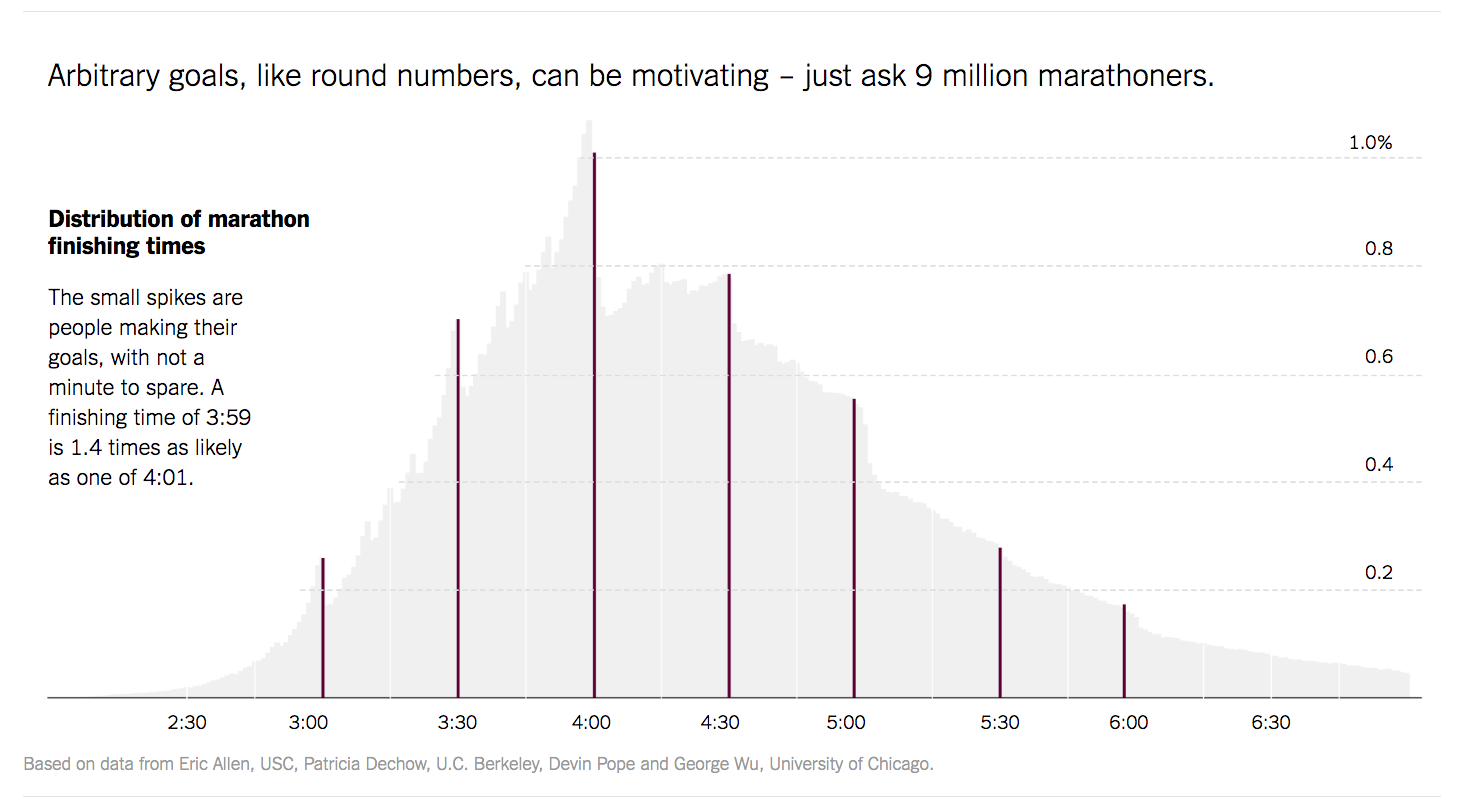
乍一看，创建直方图非常简单——我们将数据分解成几个区间，然后数下每个区间中有多少个数据。 但是，当我们仔细观察时，可以发现实际上要选择很多正确的参数才能创建一个忠实地表现数据分布形式的直方图。

如何创建直方图

收集数据

直方图是基于数值变量的数据集创建的。因此第一步就是要收集该变量的一些值来组成数据集。这里我们使用一组1974年(当然有点老了)市售车型的燃油消耗量（单位为英里/每加仑）数据作为初始数据集。我们可以将每个数据都可视化为一个对象，由其自身的值来标记——这让我们可以在理论上看到所有的数据，但也让了解数据的分布形式变得十分困难。相同数值的数据有多少？数据的波动情况怎么样？

排序

将数值按大小排序成列表是有效描述变量分布的第一步。现在我们可以看到变量中的最大值和最小值，但变量分布的中心，形状和可变性还是很不明显。造成这个问题的一个重要原因是列表变量间的距离是固定的，因此变量间的区别无法展示。这里我们需要想办法展示变量间的数值差异，了解这些变量是聚集在特定数值上或者是否有些变量与其他变量数值差异很大。

绘制数轴

使用数轴是一个常见的解决方法，数轴右侧为较大的数值而较小的或负数在左侧，最大最小数值之间的线代表了所有可能的取值。

将数据映射到数轴上

现在，我们将每个数据通过数轴映射到一个点。在右侧的可视化效果中，我们绘制了从数列到点的移动曲线，有助于表明相邻数据元素相互靠近或远离取决于其值。

在第一个样本数据集（“MPG”）中，没有两个具有完全相同值的数据。因此为了加深你的理解，我们还使用了另外两个数据集。

接下来你会看到一个极端相反类型类型的数据集，其中每个值都有很多数据点 ——”NBA”，一个包含了105名nba运动员年龄数据的数据集。年龄四舍五入到整年，所以有多个元素（即多个运动员）具有相同的年龄值。我们通过将它们堆叠在一起显示重复的值。

再往下滚动，你将看到第三个样本数据集”Geyser”，它是黄石国家公园老忠实喷泉喷发间隔时间的集合，以秒为单位。该数据集也具有多个重复的数据项—— 由于值四舍五入为整数，因此会出现这种重复性。如果时间测量精度足够高，那么数据项之间时离散的，几乎肯定不会有重复。

在这些小数据集中，点的堆叠（通常称为点图）可以让你对数据的分布有很好的理解。但是很多真实世界中的数据集中有些数值会重复数百上千次，这时候绘制所有的点变得很不实际。有时情况正相反，数据集里根本没有重复项，因此即使是数值变量的高密度区域也只会显示为数轴上不明显的一条痕迹。直方图提供了一种通过将数据聚合成组来提高可读性的方法，并且可以用于任何规模的数据集。

(可视化图表底部的按钮允许你随时在样本数据集之间切换。)

将数据切分为多组——直方图的本质

将数据点沿着数轴放置，绘制直方图涉及将数轴分成数个组并计算落入每个分组的数据项个数。要注意直方图中显示的分布如何对应点图中的分布。

将这些数据聚集到分组中有助于我们回答“这些数据的分布是什么样的？”这个问题。想象一下在电话中描述数据集：比起机械地读出整个值列表，更有效的方法是提供一个概要，比如说明变量的分布是否是对称的，是否有极端值，中心位置在哪里。直方图是另一种汇总描述方法，你可以用切分后的（例如分组）数据分布来表示整体分布。

例如，“Geyser”数据可以被描述为双峰（因为它的直方图有两个“峰值”），而“NBA”更单一，或许是右倾斜（因为组高向右下降）。

也许是因为直方图在外观上与条形图相似，很容易认为它们的客观程度也是一样的。但是与条形图不同的是，直方图受许多参数的控制。在你根据直方图中看到的内容向某人描述数据集之前，你需要知道不同的参数是否会导致你对所展示的数据集产生不同的理解。

为什么这样分组？

你可能会注意到，我们用实例数据集所作的直方图具有不同数量的分组区间。这是因为我们使用了Sturges公式，这是一种在数据集大小确定时估计直方图分组数的常用方法。

在获得一个建议的分组数后，如何确定每一组的组距呢？这里我们继续使用最常见的方法：使用最接近的整数。所以”MPG”的组距是5，”NBA”的组距是2。对于这两个数据集，这样的分组结果相当整齐的覆盖了所有数据值的范围。但看看”Geyser”的第一组和最后一组，它们的相对位置看起来有点随意，对吧？确实如此。

事实是，绘制直方图的硬性规定很少。除了Sturges的公式外，我们还可以使用Scott规则、Freedman-Diaconis规则或许多其他方法来选择分组数量。当然也没有规则说组距值必须四舍五入到2或5的最接近倍数。

重要的是给定的直方图是否是其基础数据集的代表性总结。判断这一点的一种方法是尝试改变分组边界的位置，并查看直方图传达的信息会受到什么影响。

组边界偏移

首先，我们尝试根据“偏移”设置将组边界虚线沿着数轴左右移动。观察偏移量变化时图形会发生什么变化。 数据点在从一个分组移动到另一个分组，改变了组中的数据集合，因此也改变了矩形的高度。 通常，变化的图形互相之间看起来非常相似，但偶尔会出现一个奇怪的不同形状。(将鼠标悬停在场景切换器上以控制动画。 另外还可以尝试在可用数据集之间切换。)

改变组距

我们现在将最左侧的组边界修复为最小数据值，然后改变组距。 我们在这里尝试的宽度值是根据早期阶段使用的默认组距定义的。

一些宽度值比其他选择更不适合用于某个数据集的直方图。比如说为“NBA”数据集设置1.4年的组距就会导致问题：有些分组不可避免地会跨越两个年龄取值，而其他分组只包含一个。更一般地说，箱宽度应该是测量数据所用精度的整数倍。我们的“MPG”值精确到0.1，所以对于这个数据集，1.4的宽度（英里/每加仑）就可以。

展现可视化的魔法

也许我们对公式，规则和变形的讨论让你觉得直方图是复杂的东西，需要复杂的工具。在接下来的几节中，我们会证明情况并非如此。将数据集汇总和分组，以及尝试不同的分组参数，都可以用相当简单的代码实现。

我们的代码是一系列类似公式的派生物。对于可调参数，我们提供可以选择的候选值：尝试将鼠标指针悬停在宽度行中的值上以查看具有不同组距的直方图。通过单击来将图像的组距确定为某个值。

单击该行左侧的绿色方块将打开宽度值的”扫描”界面，在该页面可以创建具有不同组距的半透明直方图云。创建扫描会为扫描影响的表的每一行添加注释。尝试创建一个扫描，然后将鼠标悬停在右侧的列上以查看各种宽度如何影响分组。

由于较宽的组区间倾向于捕获更多的数据，而较窄的区间较少，因此可能很难比较具有不同组距的直方图：狭窄的直方图形看起来太矮了。一个解决方案是将高度切换为密度——实际上绘制的是每单位数轴宽度上的数据数。可以用右图中图像下方的白色方块切换此选项。切换到密度保留了每个柱状图的总体形状，但是提高了组距较小时的图形高度（并且相反地控制了组距较大时的图形高度），使得不同组距直方图的比较更容易。使用样本数据集进行尝试，看看是否可以通过改变组距来改变整个分布的视觉”中心”。

更多调整

现在我们添加了一行，可以让你修改偏移量（请注意在修改组距时偏移量对图形分布的影响）。尝试设置宽度扫描，然后将鼠标悬停在不同的偏移值上。你可能想要切换到密度直方图以便于比较。当你探索这些参数时，你可能会遇到一个参数组合，导致分布形状大不相同。 这通常是数据规模与分组数量不匹配的结果， 有几“堆”点以一种令人意想不到的方式陷入单个分组中。

还有一件事：区间的开闭性

我们一直关注偏移量和组距的影响，但至少还有一个重要的参数：区间的”开闭性”。开闭性是关于如何处理落在分组边界上的数据。他们是被算作属于左边的组，还是属于右边的组？还是同时属于两者？肯定不是同时属于两组——因为这意味着边界上的数据项会被计算两次。在直方图中，每个数据项必须分配给一个组。

那么：更低还是更高？每个柱状图绘图工具都有一个默认策略（但可能不会透露该策略是什么，更不用说让您尝试其他替代方案）。在这篇文章中，我们的默认值是“左开”，这意味着任何具有分组左值（即，下限）的数据项都不会被算作属于该组。

左开和右开之间有多大的区别？这在很大程度上取决于数据集——特别是存在高度”堆叠”（即，大量重复）的数据值，并且刚好落在分组边界上时。在我们的样本数据集中，可以预见的是，“NBA”可能会受到区间开闭性的最大影响。（尝试使用”open”行中的绿色方块在左开和右开之间切换。请注意那些刚好落在分组边界上的数据点是如何跳跃到相邻分组的。）

所以呢？

通过以上论述，希望我们已经使你确信直方图是一种对参数选择非常敏感的图形，绘制直方图时使用可视化工具给你提供的默认参数绝对不是一个好主意。当你看到其他人制作的直方图时，你应该会好奇它们的参数是如何选定的。有些时候，作者会特意挑选参数来展示数据中实际不存在的故事。

在理想的情况下，制作直方图的人会理解参数选择如何影响他们的产出内容，查看直方图的人也会有机会了解这些参数从而说服他们自己这些图形是可信的。

我们并不认为所有直方图的制作都需要遵循上文描述的机制，但是只需要一些简单的方法就能让人们和他们的图表及控制这些图表的参数之间有更多互动。现在我们在展示用例中设置了更轻量化的控件。左右拖动图形可以调整偏移量，并且可以观察到之前存在的直方图留下的痕迹。拖动宽度控件以调整纸盒宽度。要查看直方图云，请单击扫描开关。

我们现在还加入了两个更大的数据集供你探索。

第一个是“diamonds”，一个R软件包ggplot2附带的数据集。完整的数据集包括50,000颗钻石的信息，我们只使用了其中1000颗价格较低钻石的数据。探索组距和偏移量的选择如何改变此分布的形状，中心和可变性。 （你能找到ggplot2包的作者在哪里漏掉了一页数据吗？）

第二个较大的数据集是“Marathons”，这是我们在介绍中展示的马拉松完成时间的直方图的基础数据集。来自纽约时报的直方图将近1000万马拉松选手完成时间的数据可视化。我们同样没有使用整个数据集，而是从数据中抽样，在2013年纽约市马拉松比赛中抽取3000名选手。组距较宽时，数据看起来大致对称，并且以4.5小时为中心。但是，当你减小组距时，Wolfers在纽约时报文章中描述的模式变得明显—— 马拉松选手们以整数时间为目标。尝试将鼠标悬停在某些分组上，以了解这些峰值出现的位置。 如果每个公开发布的直方图都支持这些简单的探索，是不是很美好的事？我们在此呼吁可视化软件制造商们做到这一点！

常见问题

为什么不使用核密度图？

本文主要关注直方图，这是一种对单个数值变量的分布进行可视化的方法，另一种可视化单个数值变量的流行方法是核密度图。 核密度图也能显示分布，但它们更抽象，使用一条平滑的曲线来近似表示数据分布，而不是计算每个分组中的数据样本数量。

由于它们更抽象，所以比起直方图让人感觉更“真实”，但是核密度图同样受参数的影响。 我们制作的这个快速、粗糙的R Shiny应用程序显示了基于相同数据集的核密度图也可能看起来很不一样。

使用不相等的组距会怎么样？

上文中我们还没有讨论在直方图中使用不相等的组距。如果基础数据集在某些区域比其他区域更稀疏，那么这可能是一个合适的选择——你可以在数据点稀疏的地方使用更宽的组距，在数据点密集的地方使用更窄的组距。若要使用不相等的组距，那就必须使用密度直方图而不是计数直方图，以免稀疏区域被表现的过高，因为密度直方图使用面积而非高度来表现数据项。

作为一个例子，可以看看Times发布的辣椒热量统计的等宽直方图，并与该图作者之一的另一作品(不等宽直方图)进行比较。

我可以在哪里了解直方图与平滑化的更多信息？

这取决于你想要了解到多详细的程度。 FlowingData的Nathan Yau有一篇关于直方图如何工作的文章，以及一篇关于阅读和使用R中的直方图的文章，其中包括使用了不相等组距的直方图。还有一篇面向高年级本科生或刚毕业学生水平的优秀文章是Jeffrey S. Simonoff的统计学中的平滑方法

哪些工具支持动态调整直方图的功能？

允许用户动态调整组距的弹性直方图有很多商用软件系统可以制作。 Rolf Biehler在其1997年的论文《Software for Learning and Doing Statistics》中，提到了他所开发的软件Statistics Workshop中有这样的功能。 DataDesk，Fathom和TinkerPlots中也实现了类似的功能。 然而，还是有许多专业工具不支持有弹性的直方图，有些甚至把直方图本身也抛弃了。 Excel的某些版本可以通过安装第三方附件获得创建直方图的功能，但都不支持有弹性的直方图。 R语言的专家级用户可以使用Shiny或manipulate包创建弹性直方图，但即使这些也不提供操作期间的即时反馈，而是等待用户操作结束后再更新视图。 同样的，Tableau也可以生成更新直方图参数的按钮与滑块，但是操作相当复杂。

我们是谁

我们俩(Aran Lunzer和Amelia McNamara)都热衷于让人们去探索数据。 Lunzer主要关注“虚拟界面”：一种能帮助用户理解他们需求的小变化（例如，对参数值进行微小修改，或者查询中的细微差别）是否会导致显著不同产出的展示界面。 McNamara感兴趣的是参数选择对统计可视化的影响。

如果你想分享别处发现的漂亮直方图，评论这篇文章，或者只是想问个好，都可以在推特上联系Amelia(@AmeliaMN)，或者在给aran发电子邮件,aran@acm.org。

致谢

本文的构建使用了Bootstrap的样式和提示工具，Jim Vallandingham的So You Want to Build A Scroller的滚动响应功能。 可交互的可视化效果的创建使用了D3.js和lively.lang。 如果你想了解本文所使用的代码，可以在GitHub上找到。

数据集选择按钮上的图标全部来自Noun Project：JensTärning的”Car”; Andrey Vasiliev的”Basketball”; Anton Gajdosik改编的”Fountain”; Osteea的”Diamond”; Hopkins改编的”run”。

我们也非常感谢许多同事和合作者的支持，尤其是HARC(Human Advancement Research Community)。特别要感谢MarkoRöder，Saketh Kasibatla，Yoshiki Ohshima，Chris Walker，Steve Draper，Jim McElwaine，Kathy Ahlers和Chris Baker。