倒数的诚信与消失的变量

今天朋友之间分享了一篇发表在《科学》杂志上的论文，《Civic honesty around the globe》，意即全球各地的公民诚信度。这篇论文的作者在全世界的40个国家做了一个大型的社会实验，即在不同的场所放置事先准备好的钱包，钱包中留有“主人”的联系方式，然后通过观察是否有人联系失主来推断公民的诚信程度。

这篇论文之所以受到关注，是因为大家发现文章里中国的公民诚信值位列倒数第一，于是大家纷纷吐槽，开始挖文章的实验设计。仔细一看，原来钱包里唯一的联系方式是电子邮件，而大家觉得在中国电子邮件的使用率很低，所以对文章的可信度提出了质疑。

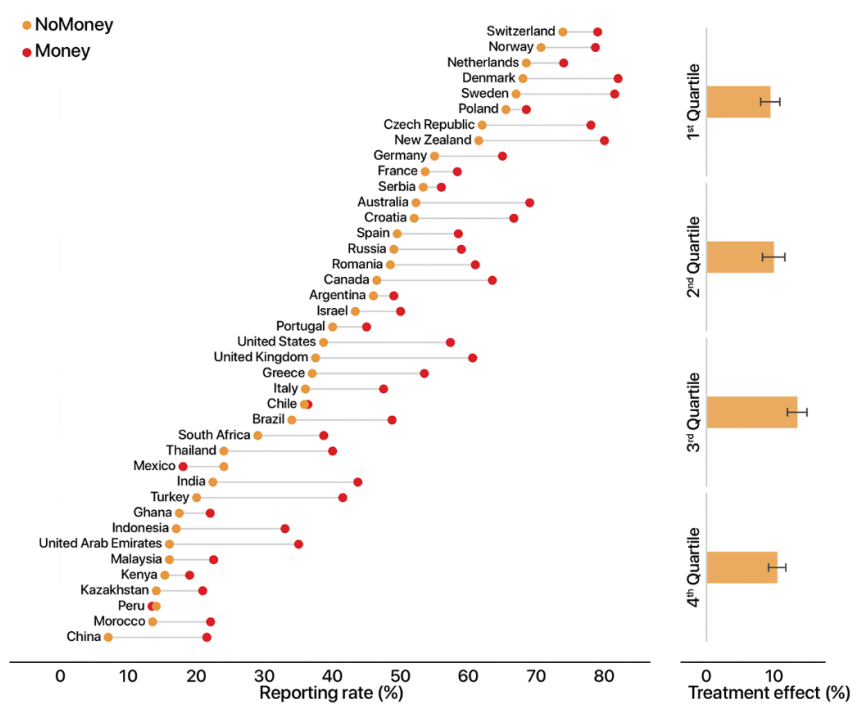
(图1：论文原文图1的钱包归还率对比。NoMoney指钱包里没有放钱，反之是有现金。)

对于这个结果，相信会有人立刻跳出来说“这是歧视”“肯定是故意的”。当然了，这种心情完全可以理解，但事实究竟是如何的呢？如果论文确实有问题，我们该如何从更科学的角度指出和证实它的缺陷？

基于这些疑问，我觉得非常有必要从统计学专业的角度来进行一些科普，目标是就问题本身进行理性的探讨，不要被带偏了方向。这里我可以先剧透一下我对这篇论文总体的看法：

1. 论文的实验设计确实存在重大的缺陷，作者背这口锅不冤；
2. 但论文的主要结论并不是国家诚信排名，而是“在几乎所有国家，钱包里的钱越多，归还的可能性越高”这一奇妙的结果；
3. 论文的作者意识到了邮件使用率这一问题，并在补充材料中进行了额外的分析。作者的结论是即使存在这一问题，图1的结果基本不受影响；
4. 对上面这点我表示怀疑，并且用作者提供的数据给出了不一样的结果。

下面我们就来挖一挖论文的统计分析过程，然后优雅地把这口锅甩给应该对其负责的人。😂这里我假定读者已经了解回归分析的基本原理，这也是论文中主要使用的分析工具。

消失的变量

我们先来回顾一下这个实验的进行过程。首先，实验者会走进一家社会机构（包含银行、文化设施、邮局、酒店和警察局五类），然后对前台说“你好，我在路上发现了这个钱包，应该是有人掉了，我现在赶时间必须要走，你能帮我处理一下吗？”。说完后实验者就会离开该机构，而后观察是否有人联系钱包中留下的电子邮箱。

这个实验的问题出在哪儿呢？很显然，对于没有收到回复的那些钱包，实验者默认它们是被机构工作人员自己留下了，也就是归入了“不诚信”的一类。但实际的情况可能是工作人员并不习惯发邮件，或是工作人员的工作非常繁忙，后来把这件事忘了，也可能是大楼里有专门的失物招领处。换言之，实验者观察到的变量是是否收到邮件，但想推断的结果却是诚信度。这两者之间并不吻合，所以需要建立一个模型来构建两者的关系。考虑一个简单的线性回归模型（注：此处更合适的模型是 Logistic 回归，但为了与论文保持一致，这里简化为线性回归），我们可以表述为

是否联系失主 = 诚信度 + b1 * 是否有失物招领处 + b2 * 是否使用邮箱 + <其他变量> + 误差

但文章所采用的模型是什么呢？很简单，就是

是否联系失主 = 诚信度 + 误差

也就是说，论文作者认为是否联系失主是诚信度的直接反应，而没有排除其他的可能性。 所以问题来了，去掉这几个变量，对结果的影响大吗？答案是，可能非常大。

逆转的符号

下面我们来做一个抽象的数值实验，来说明遗漏重要变量的后果是什么。假设我们有下面的模型，

$Y = -0.1 \cdot X_1 + 0.5 \cdot X_2 + e$

其中 $(X_1, X_2)$ 服从二元正态分布，方差都为1，相关系数为0.8，误差 $e$ 服从 $N(0, 0.1^2)$，与 $X_1$ 和 $X_2$ 独立。我们知道，在回归分析中我们通常用变量的回归系数来解释自变量对因变量的边际效应。于是，我们分别做回归 Y ~ X1 + X2 和 Y ~ X1，然后看 $X_1$ 的系数估计。

library(mvtnorm)
set.seed(123)
n = 100
x = rmvnorm(n, sigma = matrix(c(1, 0.8, 0.8, 1), 2))
x1 = x[, 1]
x2 = x[, 2]
e = rnorm(n, sd = 0.1)

y = -0.1 * x1 + 0.5 * x2 + e

summary(lm(y ~ x1 + x2))
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.011643   0.009418   1.236    0.219    
## x1          -0.093035   0.016329  -5.698  1.3e-07 ***
## x2           0.475534   0.015289  31.104  < 2e-16 ***

summary(lm(y ~ x1))
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.005001   0.031032   0.161    0.872    
## x1          0.278552   0.036685   7.593 1.85e-11 ***

可以看出，在第一个模型中，估计出的 $X_1$ 的系数非常接近真实值-0.1，而在遗漏了 $X_2$ 变量后，$X_1$ 的系数估计变成了0.278，符号直接被反转了！如果我们草率地从第二个结果中得出结论“$X_1$ 对 $Y$ 有正向的影响”，那就非常危险了。类似地，在论文当中如果要研究诚信度与国家之间的关系，那么排除掉重要变量也可能使得结果的排名发生巨大的变化。

还能再抢救一下吗？

既然有遗漏重要变量的可能，那么有什么补救的措施吗？简单来说，有，但恐怕还远远不够。

回到我们之前的诚信度模型，非常遗憾作者并没有去调查失物招领和邮件使用这两个重要变量。未观测到的变量就永远丢失了，而剩下的希望就是寻找这些变量的替代者。事实上，论文作者在其补充材料中确实这么做了，他们在实验中还观测了一些其他的变量，例如工作人员身边是否有电脑，以及工作人员周边是否有其他人等。特别地，考虑到不同国家的电子邮件普及率不同，作者还从世界银行的数据库获取了若干国家的商务邮件使用率，然后加入到补充材料的模型当中。在加入了这些新的变量后，论文作者绘制了如下调整后的归还率，其中由于许多欧美国家的数据缺失，所以只对剩下的国家进行了计算。

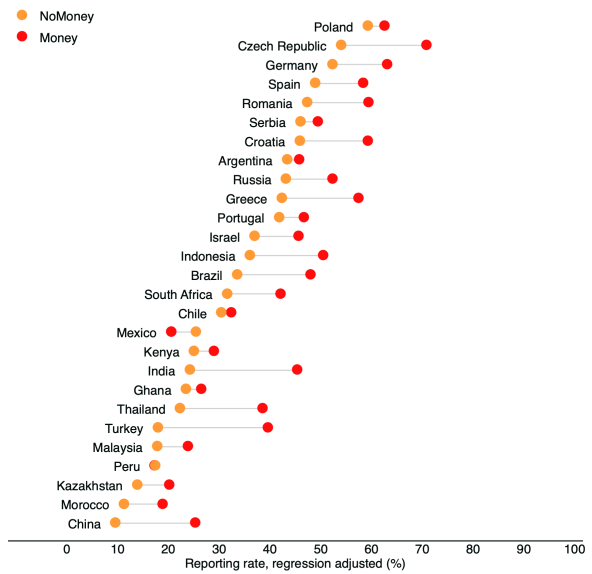
(图2：论文原文图S14的调整后钱包归还率。)

论文作者发现，这个结果与之前的图1相差不大，所以认为邮件使用率并不是一个大的影响因素。然而，我们发现这其中依然问题很大。首先，一些重要的变量，如失物招领处，依然没有合适的替代者。其次，论文中使用的邮件使用率是针对跨国公司的商务邮件调查，对普通人的交流习惯几乎没有特别大的指导意义。事实上对于中国来说，跨国公司商务邮件的使用率高达85%，但我们很难想像现实生活中会有这么高的电子邮件使用率。由于论文中的实验发生在2015年，我们研究了中国互联网络信息中心的第36次《中国互联网络发展状况统计报告》。报告指出，在2015年6月，中国电子邮件的用户规模为2.4亿人，对应网民使用率36.7%。而在手机网民这个子群里中，手机即时通信的用户规模为5.4亿，使用率则达到了惊人的91%。这两者之间巨大的差异让我们猜测，替代变量的质量可能会极大影响调整的效果。

以彼之道

为了验证我们的想法，我们决定使用论文作者的模型进行一项额外的分析。值得赞许的是，这篇论文提供了非常详尽的原始数据，这使得我们可以重现论文中的各种结果。我们采用和图2相同的模型，但分析的对象是欧洲的国家，原因如下：

1. 欧洲国家正好与图2互补，因此相当于进行了一次独立的实验；
2. 欧盟官方网站提供了一份调查数据，调查内容是询问年龄在16到74之间的被调查者在过去的三个月内是否使用过电子邮件。这项调查针对的是普通民众，因此代表性更强；
3. 欧洲国家之间的文化差异相对图2中的国家更小，因此结果的可信度应该更高。

本文最后给出了分析所用的 R 代码，以下是结果的展示。

(图3：对欧洲国家计算的调整后钱包归还率。)

从图3中我们可以很明显地看到调整后的两大趋势：

1. 原来国家之间的巨大差异被缩小了；
2. 原来明显的排序被打乱了。

最有戏剧效果的是土耳其和英国之间的对比。我猜这两位此时的心情应该是这样的：

需要强调的是，我们依然不认为我们图3中的结果是准确的，因为仍旧有重要的变量遗失。图3的意义在于，我们使用了作者提供的调查结果和一组额外更可靠的数据，进行了相同的统计分析，却得到了与作者不一样的结论。这恰恰说明，关键变量的准确测量对分析结果的影响是极其巨大的。

未雨绸缪

前面说了这么多补救措施，但其实最佳的方案仍然是在收集数据前进行细致及合理的实验设计。说到实验设计的黄金准则，大家第一反应可能都是“随机对照实验”（即，把实验对象随机分配，然后一组接受处理，另一组什么都不做，比较两组差别就可以得出处理单因素对于结果的影响）。当然能做随机对照实验固然是好，只是不是所有问题都可以用随机对照实验来回答（比如原文中随机发放的“有钱的钱包”和“没钱的钱包”就是一个随机对照实验，可以用来回答“有没有钱”对于归还率的影响）。

实验设计的初衷，其实就是尽可能地排除各种潜在的共生因素，从而剥离出来处理本身对于结果的影响。大家都知道，在可以做随机对照的情况下，其实分析模型里面是不需要加入其他可能的因素的。那么在不可以做随机对照实验的时候，我们如何借鉴这种想法，让实验本身更可靠呢？

在本例中，实验设计者其实有用心地去改良实验设计，以尽可能地减少其他因素对于归还率的影响。比如在选择投放钱包的地点的时候，他们刻意地规避了“相邻或者隔街相望的地点”（excluded drop-off locations that were next to or across the street from one another），从而避免路人对这是一个恶作剧（社会实验）的怀疑（即“霍桑效应”，如果被测试者知道这是一个实验，有可能表现出与平时反应不同的行为）。又比如，实验设计者使用的是“透明的钱包”，这样被测试者不需要打开钱包就可以大概知道里面的内容。里面放置的购物清单、使用每个国家常见的名字等等，更容易让人认为失主是当地人，而不是过路的旅行者（避免被测试者假设就算联系到了失主也无法归还，从而降低联系失主的概率）。

实验设计者虽然精心控制了很多因素的影响，但这毕竟是跨越四十个国家的社会实验，很难保证没有瑕疵。实验设计中没有尽力控制的因素，如果对归还率有潜在的影响，那么就会影响到最终对于“诚信度”的判断。在各国网友的热切反馈中，以下列举了实验中没有控制的因素：

1. 各国最通行的联系手段。在某些西方国家比如英美，大家可能习惯于电子邮件沟通，而在其他很多地方，可能很多人几乎就不使用邮箱（比如现在的大学生可能靠微信来联系老师，而不是传统的电子邮件）。本实验中，被测试者大都是前台接待人员，假设他们代表国民平均水平的话，显然是否信任电子邮件这种联络方式会对归还率有潜在的影响。这也是被大家最诟病的。
2. 投放钱包的人只有13位，大都是德国大学的学生。虽然原文中没有更多关于这些学生的信息，但是很可能的是，他们在某些国家看起来更像“外国人”，而在欧洲本地可能更像是欧洲人。作者在分析中虽然考虑了控制这些学生的个体因素，但是他们并没有进一步考量每个学生相对于投放所在国的“外国人”效应。
3. 其他失物招领手段。在某些国家，可能社会通行的做法是会主动联系失主，而有些国家，可能通行的做法是默认失主会回到原地寻找财物。这也会对归还率有影响。
4. 前台接待人员的代表性。在有些国家，前台接待人员可能会有比一般民众更高的受教育程度，而在其他国家则不一定。
5. 钱包内容。虽然实验设计在不同国家使用了相同的钱包内容以排除内容的影响，但不同国家对于内容的重要性的认知可能是不一样的。归还率可能不仅仅被诚信度影响，还可能被人们“慵懒度”影响，如果他们主观认为丢失的东西不太重要的话。
6. 城市人口的影响。实验者虽然选择的是每个国家有代表性的城市，但是显然，一个人口超过三千万的中国城市和一个北欧的“大城市”之间的人口还是有着量级的差别的。当人口规模很大的时候，被试验者可能假设归还成功的概率很低，从而降低他们联系失主的意愿。
7. 奇怪的钱包。实验者使用的是透明的“名片包”，而非人们日常使用的真正的钱包，这可能会影响被试验者对于钱包重要度甚至“恶作剧”的主观判断。

有些因素可以在回归中引入控制变量（比如通信手段），而有些因素则很难量化，从而和“诚信度”一起成为无法观测的变量，被归入到回归模型的残差项之中。

结语

经过我们的分析我们可以发现，即使是发表在《科学》这样顶级期刊的文章，依然存在重大的逻辑漏洞。虽然论文作者并未把国家的诚信排名作为其主要结论，但在正文中作者也确实没有对“诚信度”的涵义进行详细的解释，而且对于这类容易引起争议的结果缺乏必要的澄清。从统计的角度来看，研究者对于实验设计的重视程度还远没有到令人满意的程度，而对分析结果的不谨慎和滥用也很可能会违背科学研究的基本原则。我们衷心希望的是，在利用统计分析研究诚信问题时，不要让统计成为了谎言的工具。

注：本文的内容是和统计之都文章《假新闻引发的愤怒——非算法视角对自我学习的搜索排序算法和选择偏差的一些解读》的作者共同讨论决定的，正是该文对于“选择偏差”的论述启发了本文的写作。

附录：图3的R语言分析代码

相关数据文件可在 https://github.com/cosname/uploads/tree/master/2019/06 下载得到。

library(readr)
library(dplyr)
library(ggplot2)

raw = read_csv("honesty_data.csv") %>%
    filter(cond < 2) %>%
    select(response, cond, male, above40, computer, coworkers,
           other_bystanders, institution, Country) %>% na.omit
email = read_csv("eu_email.csv")
dat = raw %>% inner_join(email, by = "Country")

## Reproduce the result in the paper
res = dat %>% group_by(Country, cond) %>%
    summarize(rate = mean(response)) %>%
    arrange(cond, rate) %>% as.data.frame
ordering = res$Country[res$cond == 0]

ggplot(res, aes(x = rate, y = Country, color = factor(cond))) +
    geom_point(size = 3.5) +
    scale_y_discrete(limits = ordering) +
    scale_color_hue("", labels = c("NoMoney", "Money")) +
    xlab("Original Rate") + xlim(20, 90) +
    theme_bw(base_size = 20) +
    theme(legend.position = "top", axis.title.y = element_blank())


## Include control variables
## No money case
dat0 = dat %>% filter(cond == 0)
mod0 = lm(response ~ email + male + above40 + computer + coworkers +
              other_bystanders + institution, data = dat0)
drop1(mod0, test = "Chisq")
dat0$resid = residuals(mod0)
res0 = dat0 %>% group_by(Country) %>%
    summarize(rate = mean(resid)) %>%
    arrange(rate) %>% as.data.frame
res0$rate = res0$rate + mean(dat0$response)
res0$cond = 0
## Money case
dat1 = dat %>% filter(cond == 1)
mod1 = lm(response ~ email + male + above40 + computer + coworkers +
              other_bystanders + institution, data = dat1)
drop1(mod1, test = "Chisq")
dat1$resid = residuals(mod1)
res1 = dat1 %>% group_by(Country) %>%
    summarize(rate = mean(resid)) %>%
    arrange(desc(rate)) %>%
    as.data.frame
res1$rate = res1$rate + mean(dat1$response)
res1$cond = 1

res_adj = rbind(res0, res1)
ordering_adj = res_adj$Country[res_adj$cond == 0]

ggplot(res_adj, aes(x = rate, y = Country, color = factor(cond))) +
    geom_point(size = 3.5) +
    scale_y_discrete(limits = ordering) +
    scale_color_hue("", labels = c("NoMoney", "Money")) +
    xlab("Adjusted Rate") + xlim(20, 90) +
    theme_bw(base_size = 20) +
    theme(legend.position = "top", axis.title.y = element_blank())